Bild und Kern einer Koeffizientenmatrix bestimmen

Question

Aufgabe:

Folgendes LGS:

I   x + 3y - z = 3

II 2x +     7z = 4

1. Bestimme Bild und Kern der zugehörigen Koeffizientenmatrix

Problem/Ansatz:

Ich habe erstmal einfach gemäß $$A*x^{Vektorpfeil}= b^{Vektorpfeil}$$ eine Koeffizientenmatrix und eine erweiterte Koeffizientenmatrix aufgestellt.

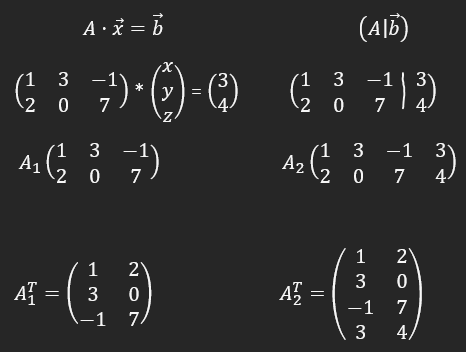
Text erkannt:

\( A \cdot \vec{x}=\vec{b} \)
\( \left(\begin{array}{ccc}1 & 3 & -1 \\ 2 & 0 & 7\end{array}\right) *\left(\begin{array}{l}x \\ y \\ z\end{array}\right)=\left(\begin{array}{l}3 \\ 4\end{array}\right) \)
\( A_{1}\left(\begin{array}{ccc}1 & 3 & -1 \\ 2 & 0 & 7\end{array}\right) \)
\( \left(\begin{array}{ccc|c}1 & 3 & -1 & 3 \\ 2 & 0 & 7 & 4\end{array}\right) \)
\( A_{2}\left(\begin{array}{cccc}1 & 3 & -1 & 3 \\ 2 & 0 & 7 & 4\end{array}\right) \)
\( A_{1}^{T}=\left(\begin{array}{cc}1 & 2 \\ 3 & 0 \\ -1 & 7\end{array}\right) \quad A_{2}^{T}=\left(\begin{array}{cc}1 & 2 \\ 3 & 0 \\ -1 & 7 \\ 3 & 4\end{array}\right) \)

Mein Ansatz ist folgender:

1. Matrix transponiert (wie auf dem Bild)

2. Matrix in obere Dreiecksmatrix umwandeln (Gauß)

3. zurücktransponieren

4. die Spalten wo nicht nur Nullen vorkommen gehören zur Matrix

Jetzt bin ich aber bei folgendem Problem:

Ich habe die Matrix transponiert allerdings weiß ich nicht welche ich von den beiden A_1 oder A_2 ich nutzen soll. Und dann wie ich Gauß auf eine 2x4 Matrix anwenden soll.

Ich freue mich über jede Hilfe!

Answer 1

Aloha :)

Willkommen in der Mathelounge... \o/

Die Koeffizientenmatrix lautet:$$A=\left(\begin{array}{rrr}1 & 3 & -1\\2 & 0 & 7\end{array}\right)$$Das Bild bestimmst du, indem du die linearen Abhängigkeiten aus den Spaltenvektoren herausrechnest. Das geht z.B. mit elementaren Spaltenumformungen:$$\begin{array}{rrr} &\colon3& \\\hline1 & 3 & -1\\2 & 0 & 7\end{array}\to\begin{array}{rrr} -S_2 & & +S_2 \\\hline1 & 1 & -1\\2 & 0 & 7\end{array}\to\begin{array}{rrr} \colon2 & & \\\hline0 & 1 & 0\\2 & 0 & 7\end{array}\to\begin{array}{rrr} & & -7S_1\\\hline0 & 1 & 0\\1 & 0 & 7\end{array}\to\begin{array}{rrr} & & \\\hline0 & 1 & 0\\1 & 0 & 0\end{array}$$Es bleiben die beiden Basis-Vektoren des \(\mathbb R^2\) übrig. Das Bild der Matrix ist also \(\mathbb R^2\).

Den Kern der Koeffizientmatrix findest du, indem du alle Vektoren \(\vec x\) bestimmst, die mulitpliziert an die Matrix den Nullvektor ergeben:$$A\cdot\vec x=\vec 0$$Das formulieren wir als Gleichungssystem:$$\begin{array}{rrr|r|l}x_1 & x_2 & x_3 & = &\text{Aktion}\\\hline1 & 3 & -1 &  0 & \\ 2 & 0 & 7 & 0 &-2\cdot\text{Zeile 1}\\\hline1 & 3 & -1 &  0 & \\ 0 & -6 & 9 & 0 &\colon(-6)\\\hline1 & 3 & -1 &  0 & -3\cdot\text{Zeile 2}\\ 0 & 1 & -1,5 & 0 &\\\hline1 & 0 & -3,5 &  0 &\\ 0 & 1 & -1,5 & 0 &\end{array}$$Unser Ziel haben wir erreicht, nämlich so viele Spalten wie möglich zu erzeugen, die lauter Nullen mit genau einer Eins enthalten. Daraus lesen wir nämlich nun 2 Gleichungen ab:$$x_1-3,5x_3=0\;\text{bzw.}\;x_1=3,5x_3\quad\text{und}\quad x_2-1,5x_3=0\;\text{bzw.}\;x_2=1,5x_3$$und können damit alle Lösungen bzw. den Kern der Matrix angeben:$$\begin{pmatrix}x_1\\x_2\\x_3\end{pmatrix}=\begin{pmatrix}3,5x_3\\1,5x_3\\x_3\end{pmatrix}=x_3\begin{pmatrix}3,5\\1,5\\1\end{pmatrix}$$

Comments

Vielen, vielen Dank! Ich hatte es selber danach nochmal versucht und es hat gefunt.