Differentialrechnung zur Berechnung eines Rechtecks vom Umfang 30cm und kürzester Diagonale?

Question

Hallo liebe Mathe cracks,

Mir brennt eine Frage auf dem Herzen,

Aufgabe;

Welches Rechteck mit einem Umfang von 30 cm hat die kürzeste Diagonale?

Mehr ist nich angegeben.

Answer 1

Ich bin kein Mathecrack, aber
sich zu denken, dass ein Quadrat die kürzeste Diagonale hat
und das diese nur länger werden kann wenn man die Länge einer
beliebigen Seite bei gleichbleibendem Umfang ändert,
ist nicht gerade ein Crackthema. :P

2a + 2b = 30
b = 15 - a

d(a) = √(a^2 + b^2)
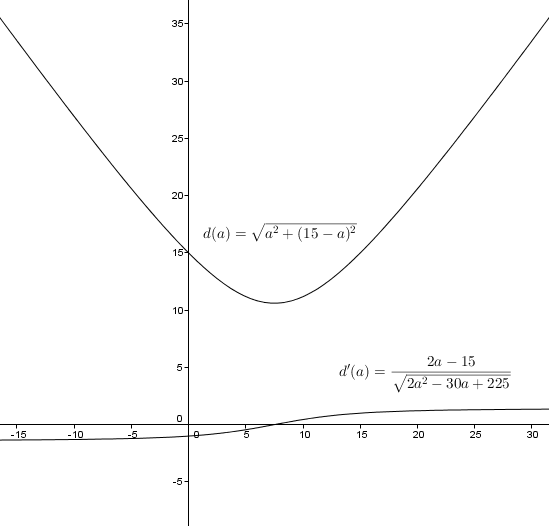
d(a) = √(a^2 + (15 - a)^2)
d(a) = √(a^2 + 15^2 - 30a + a^2)
d(a) = √(2a^2 - 30a + 225)

d'(a) = 1/2 (2a^2 - 30a + 225)^{-1/2} (4a - 30)
d'(a) = (2a - 15)/√(2a^2 - 30a + 225)

Gesucht ist a, sodass d(a) minimal wird.
d'(a) = 0
(2a - 15)/√(2a^2 - 30a + 225) = 0

Dieser Bruch wird Null, wenn der Zähler Null wird.
Dabei darf der Nenner nicht Null werden, weil wir sonst
einen unbestimmten Ausdruck hätten.
Bei welchem a wird der Nenner Null?
Das erfahren wir, indem wir die quadratische Gleichung 2a^2 - 30a + 225 = 0 lösen.

2a^2 - 30a + 225 = 0
a^2 - 15a + 112.5 = 0
a_1,2 = √((7.5)^2 - 112.5)
a_1,2 = √(-56,25)

Der Nenner kann nicht Null werden, weil die quadratische Gleichung
im Reellen keine Lösung hat und weil uns nur Lösungen innerhalb der
Menge der reellen Zahlen interessieren.
Wir können also unbekümmert :P den Zähler Null setzen:

2a - 15 = 0
a = 15/2
a = 7.5

Haben wir bei a = 7.5 ein Minimum?
d''(a) = 225/(2a^2 - 30a + 225)^{3/2}
d''(7.5) = 0.189
d''(7.5) > 0 ⇒ jepp, bei a = 7.5 ist die Diagonale d minimal.

Welche Länge hat b, wenn a = 7.5(cm) lang ist?
b = 15 - a = 15 - 7.5
b = 7.5

a = b = 7.5 ⇒ unser gesuchtes Rechteck ist ein Quadrat ⇒ Uiiii! Welch Überrachung! :D :P

 

Comments

Schöne Antwort!

Man dürfte auch das Quadrat der Diagonalen minimieren, denn Quadrat der Länge und Länge einer Strecke sind unter den gleichen Bedingungen minimal. So spart man die Ableitung der Wurzelfunktion.

---

:-)
Das Quadrat der Diagonalen zu minimieren ist ein sehr guter Tipp!
Auf diese Idee kam ich leider nicht, nach durchgemachter Disconacht.

Answer 2

Hi,

die Diagonale ist dann am kleinsten, wenn alle Seiten gleich sind. Die Summe von allen Seiten soll 30cm sein. Wenn die Seiten nicht gleich lang sind, ist die Diagonale ja auch nicht minimal. Das bedeutet also: Vier gleich lange Seiten sollen in der Summe 30cm sein. Wenn du dir nun ausrechnest, wie lang eine Seite ist, kannst du über den Satz des Pythagoras dir ausrechnen, wie lang die Diagonale ist.

Comments

Hi

ok, dann wäre eine Seit 7,5 cm lang wenn die These stimmt.

denn 4 Seiten x 7,5cm  = 30 cm.

Die Diagonale A² x B² = 900 

oder so ähnlich

---

Das mit dem Satz von Pythagoras war allerdings ein  bisschen anders