Hallo Nita,
mache Dir immer eine Skizze:
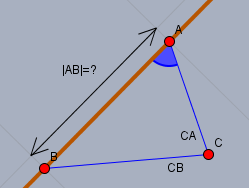
Der Cosinussatz, der sich am Winkel \(\angle CAB\) (blau) orientiert, lautet hier:$$|CB|^2 = |AB|^2 + |CA|^2 - 2|AB|\,|CA|\cos(\angle CAB)$$Das Quadrat der Seite (hier \(CB\)), die dem Winkel \(\angle CAB\) gegenüber liegt, steht immer alleine auf der hier linken Seite der Gleichung.
Bis auf \(|AB|\) sind in der Aufgabenstellung alle Größen gegeben. Folglich lässt sich \(|AB|\) berechnen aus:$$|AB|_{1,2} = |CA|\cos(\angle CAB) \pm \sqrt{|CA|^2\cos^2(\angle CAB) + |CB|^2-|CA|^2} \\ \phantom{|AB|_{1,2}}= |CA|\cos(\angle CAB) \pm \sqrt{|CB|^2 - |CA|^2(1-\cos^2(\angle CAB))}\\ \phantom{|AB|_{1,2}}= |CA|\cos(\angle CAB) \pm \sqrt{|CB|^2 - |CA|^2\sin^2(\angle CAB)}$$Wie man sieht, gibt es zwei Lösungen. In diesem Anwendungsfall hat wahrscheinlich eine der beiden Lösungen ein negatives Vorzeichen. Diese kann man dann vernachlässigen.
Falls Du Fragen dazu hast, so melde Dich bitte.
Gruß Werner
