Aufgabe:
Aufgabe 4.
Sei K = R und V = R2. Für die Addition + auf V w ählen wir die übliche Vektoraddition,
aber die Skalarmultiplikation ändern wir subtil ab:
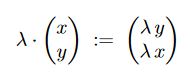
Text erkannt:
\( \lambda \cdot\left(\begin{array}{l}x \\ y\end{array}\right):=\left(\begin{array}{l}\lambda y \\ \lambda x\end{array}\right) \)
Die Koeffizienten werden also bei jeder Skalarmultiplikation ausgetauscht.
Prüfen Sie, welche Eigenschaften aus der Definition eines Vektorraums für diese Kombination (V,+,·) noch erfüllt sind und welche nicht.
Problem/Ansatz: Ich habe keine Ahnung wie ich was machen soll und brauche Hilfe.
Text erkannt:
\( \lambda \cdot\left(\begin{array}{l}x \\ y\end{array}\right):=\left(\begin{array}{l}\lambda y \\ \lambda x\end{array}\right) \)
