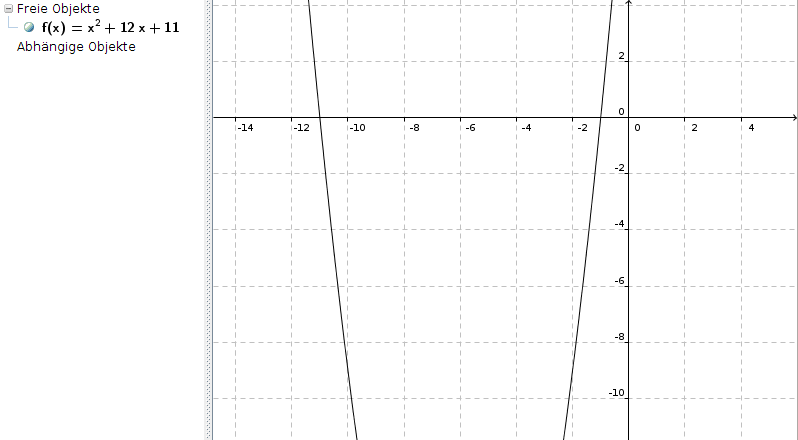
zur Überprüfung, ob P(2|39) auf der Parabel liegt, setzen wir einfach die Koordinaten in die Funktionsgleichung ein:
y = x2 + 12x + 11
39 = 4 + 24 + 11 = 39
Wahre Aussage, der Punkt P liegt also auf der Parabel.
Nullstelle mittels pq-Formel:
x1,2 = -6 ± √(36-11) = -6 ± √25 = -6 ± 5
x1 = -1
x2 = -11
Besten Gruß