Zeigen Sie, dass die Reihe konvergiert und geben Sie Reihenwert an.

Question

Aufgabe: Ziegen Sie, dass die Reihe konvergiert und geben Sie den Reihenwert an.

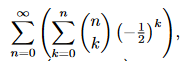
Text erkannt:

\( \sum \limits_{n=0}^{\infty}\left(\sum \limits_{k=0}^{n}\left(\begin{array}{l}n \\ k\end{array}\right)\left(-\frac{1}{2}\right)^{k}\right) \)

Problem/Ansatz:

Ich würde hier den binomischen Lehrsatz verwenden. Wie soll ich das (-1/2)^k, auf den Satz x^n-k y^k anwenden?

Vielen Dank vorab

Comments

Betrachte mal ( 1 - (1/2) ) ^n

einmal nach dem binomischen Satz und

einmal durch direktes ausrechnen ( 1 - (1/2) ) ^n = (1/2)^n

---

Wir brauchen doch für die Umformung (x+y)ⁿ die Form x^n-k · y^k . Wenn y^k = (-1/2)^k wie muss ich das x^n-k wählen?

---

Das x ist doch dann die 1, und die hoch irgendwas gibt immer

1, kann also als Faktor wegfallen.

Answer 1

Setze y=-1/2 und x=1 dann gibt die innere Summe \(1/2^n\)

Dann die geometrische ⁹Reihe verwenden.