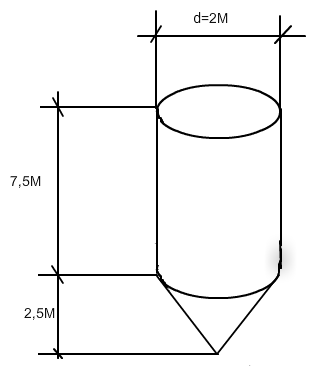
Ein Getreidesilo besteht aus zwei Bereichen. Der untere Abschnitt ist ein auf dem Kopf stehender Kegel; er hat einen Durchmesser von zwei Metern und eine Höhe von 2,5 Meter. Der zylindrische obere Teil hat denselben Durchmesser und eine Höhe von 7,5 Meter. An der Außenseite soll eine Füllstandsanzeige angebracht werden, bei der das Füllvolumen abgelesen werden kann.
1. Wie lautet die Gleichung der Funktion V : h |-> V(h),die das Volumen V in Abhängigkeit von der Füllstandshöhe h beschreibt?
2. Welchen Definitionsbereich hat diese Funktion?
3. In welchen Abständen müssen im unteren Bereich die Markierungen angebracht werden, damit die Füllstände im Abstand von 1m³ abgelesen werden können?
4. In welchem Abstand müssen im oberen Bereich die Markierungen angebracht werden für einen Abstand der Füllstände von 5m³?
Ich komme bei Aufgabe Nummer 1 nur auf eine Funktion ersten Gerades dabei nehmen wir im Unterricht gerade die dritten Gerades durch. Vlt könnt ihr mir helfen?
Mein Lösungsweg :
V(h)= [(π*r²*h)+(π/3*r²*h)]
V(h)= [(π*r²)+(π/3*r²)]*h
V(h)= [(π*1²)+(π/3*1²)]*h
V(h)= [π+π/3]*h
V(h)= (1 1/3π)*h