Zu beweisen sind ein Satz und seine Umkehrung:
Ein Punkt, der den gleichen Abstand von den Schenkeln eines Winkels hat, liegt auf der Winkelhalbierenden.
g und h seien die Schenkel eine Winkels und P ein Punkt in der Ebene von g und h:
Das Lot von P auf g hat den Fußpunkt A. Das Lot von P auf h hat den Fußpunkt B.
Wenn PA= PB, dann stimmen die Dreiecke ABP und SPA in der Länge einer Seite, der Größe des gegenüberliegenden Winkels der längen Seite und der Länge einer anliegenden Seite des Winkels überein.
Dann sind die Dreiecke ABP und SPA kongruent und stimmen in allen Winkel überein, insbesondere in α und β.
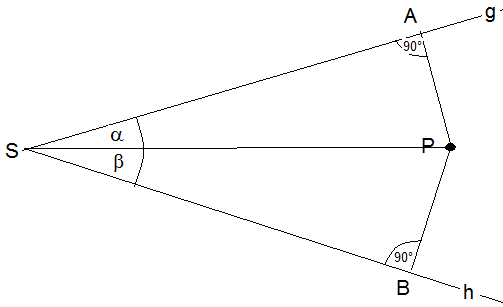
Also halbiert SP den Winkel α+β.
Nun noch die Umkehrung beweisen.