Hallo,
Willkommen in der Mathelounge!
Daraus bekomme ich dann das LGS
12s-6r=-4
4s-12r=4
3s-4r=-1
das ist richtig,
Wenn ich die jedoch löse bekomme ich im Taschenrechner keine Lösungen
das ist auch richtig ;-) Wenn sich die Bahnen nicht schneiden, also keinen gemeinsamen Punkt haben, kann es auch keine Lösung für drei Gleichungen mit nur zwei Unbekannten geben.
Um den 'Kreuzungspunkt' in der horizontale Ebene zu berechnen, so löse das Gleichungssysten für die xy- (bzw \(x_1\,x_2\))-Koordinate. Das sind die ersten beiden Gleichungen:$$12s-6r=-4\\ 4s-12r=4 \\\implies s=-\frac{3}5,\quad r=-\frac{8}{15}$$setze dies in die beiden Geradengleichungen ein und Du kommst zu den Punkten aus der Lösung.
Hier noch die Szene im Geoknecht3D
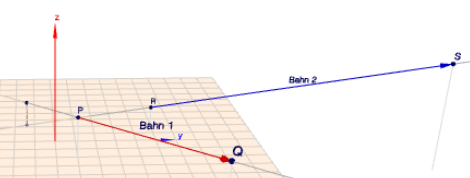
(klick auf das Bild)
Gruß Werner