\(f(x)=\frac{1}{x}\)
a) Verwende einen Funktionsplotter, um den Graphen zu skizzieren, oder deinen TR:
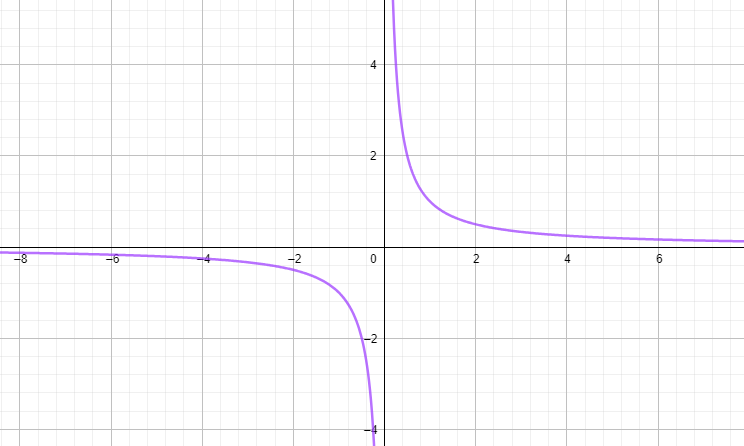
b) Potenzregel \(\frac{1}{x^m}=x^{-m}\), also \(f(x)=x^{-1}\)
c) Schnittpunkte mit den Koordinatenachsen:
Die Funktion schneidet weder die x- noch die y-Achse.
Schnittpunkt y-Achse: Du kannst für x nicht Null einsetzen, weil der Nenner eines Bruches nie Null werden darf.
Schnittpunkt x-Achse: Setze die Funktion = 0 und löse nach x auf:
\(\frac{1}x{}=0\\1=0\) Widerspruch, daher auch hier kein Schnittpunkt.
d) Alle reellen Zahlen außer der Null
e) \(f(x)=x^{-1}\\f'(x)=-1\cdot x^{-1-1}=-x^{-2}\;\text{oder}\;-\frac{1}{x^2}\)
Melde dich, falls du dazu noch Fragen hast.
Gruß, Silvia