Aufgabe:
Es sei \( D_{4} \) die Menge der Symmetrien des Quadrats
\( Q:=\left\{s\left(\begin{array}{l} 1 \\ 0 \end{array}\right)+t\left(\begin{array}{l} 0 \\ 1 \end{array}\right): s, t \in \mathbb{R},|s|+|t|=1\right\} \)
Das heißt, dass \( D_{4} \) die Menge der Drehungen und Spiegelungen im \( \mathbb{R}^{2} \) ist, die \( \mathrm{Q} \) auf \( \mathrm{Q} \) abbilden. Einen Teil der Elemente von \( D_{4} \) sind in der folgenden Grafik veranschaulicht:
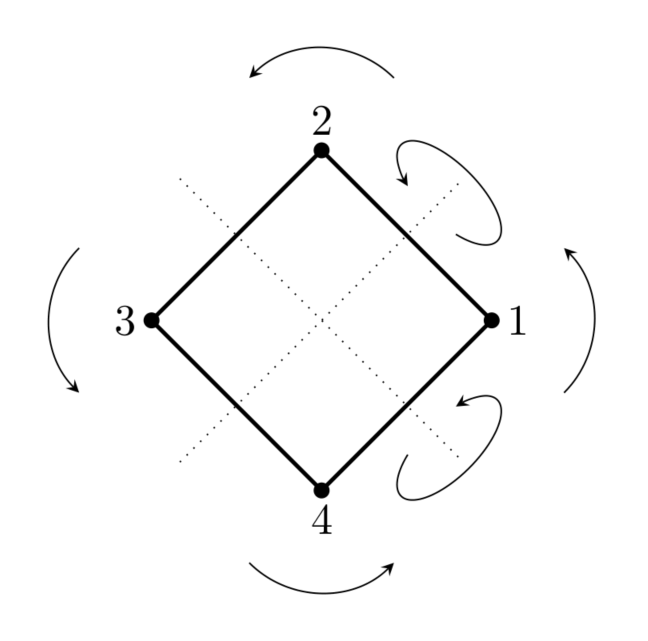
Zusammen mit der Komposition o von Abbildungen bildet \( \left(D_{4}, \circ\right) \) eine Gruppe.
a) Bestimmen Sie die Anzahl der Elemente in \( D_{4} \cdot\left|D_{4}\right|= \)
b) Ist \( \left(D_{4}, 0\right) \) eine abelsche Gruppe? Antwort:
(Tragen Sie "ja" oder "nein" in das Antwortfeld ein!)