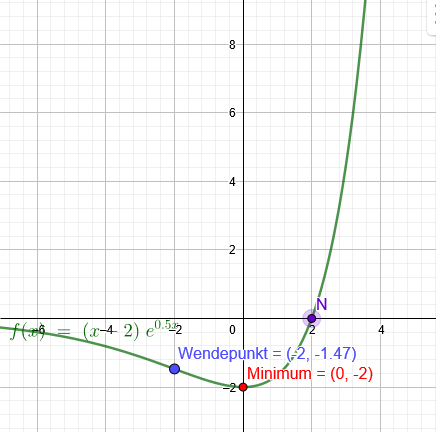
f(x)= (x-2)*\( e^{0,5x} \)
Ich soll die Definitionsmenge, Symmetrie, Definitionsmenge, Extremstellen und Wendepunkte herausfinden.
f(x) ist überall definiert.
Untersuchung auf Achsensymmetrie zur y-Achse:
f(x)= (x-2)*\( e^{0,5x} \)
f(-x)= (-x-2)*\( e^{-0,5x} \)
f(x)≠f(-x)
Untersuchung auf Punktsymmetrie zum Ursprung:
f(-x)= (-x-2)*\( e^{-0,5x} \)
-f(x)= -(x-2)*\( e^{0,5x} \)
f (−x)≠− f (x )
Es liegt keine Symmetrie vor.
Nullstelle: x=2
Extremstellen:
f´(x)= \( e^{0,5x} \)+ (x-2)*\( e^{0,5x} \)*0,5
\( e^{0,5x} \)+ (x-2)*\( e^{0,5x} \)*0,5=0
\( e^{0,5x} \)*(1+0,5x-1)=0
\( e^{0,5x} \)*(0,5x)=0
x=0 f(0)= (0-2)*\( e^{0,5*0} \)=-2
Art des Extremwertes:
f´´(x)= \( e^{0,5*x} \)*(0,25x+0,5)
f´´(0)= \( e^{0,5*0} \)*(0,25*0+0,5)=0,5>0 Minimum
Wendepunkt:
\( e^{0,5*x} \)*(0,25x+0,5)=0
0,25x+0,5=0
x=-2
f(-2)= (-2-2)*\( e^{0,5*(-2)} \)=-1,47