Hallo,
EIne Tangentialebene an eine Funktion mit zwei Parametren ist eine Linearisierung der Funktion in einem gewählten Punkt. Die Funktion $$f(x,y) = (x^2+y^2)e^{-x}$$kannst Du Dir wie ein Höhenprofil in der Landschaft vorstellen, bei dem für jedem Punkt \((x,\,y)\) eine Höhe \(f(x,\,y)\) vorgegeben ist. Gibt man sich das z.B. mit Wolfram Alpha als Plot aus, so erhält man so etwas:
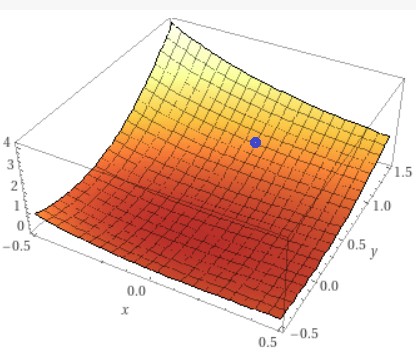
Die Position \(P(0|\,1)\) habe ich als blauen Punkt markiert. Beachte bitte, dass die vertikale Achse gegenüber der X- und Y-Achse stark gestaucht ist. Das 'Gelände' ist also steiler als es hier scheint.
Die Linearisierung funktioniert wie im eindimensionalen Fall, nur eben in zwei Richtungen$$z(x,y) = f(p) + f_x(p)(x-x_p) + f_y(p)(y-y_p) \\ f(p) = f(0,1) = 1 \\ f_x(p) = \frac{\partial f}{\partial x}(0,1) = (2x - x^2-y^2)e^{-x} = -1 \\f_y(p) = \frac{\partial f}{\partial y}(0,1) = 2ye^{-x} = 2$$wandelt man dies um, entsteht daraus die Normalform einer Ebene$$\begin{aligned}z &= f(p) + f_x (x-x_p) + f_y (y-y_p) \\ -f_x x - f_yy + z &= - f_xx_p -f_yy_p + f(p)\\ \begin{pmatrix} -f_x\\ -f_y\\ 1\end{pmatrix} \vec x &= \begin{pmatrix} -f_x\\ -f_y\\ 1\end{pmatrix} \begin{pmatrix} x_p\\ y_p\\ f(p)\end{pmatrix}\end{aligned}$$einsetzen der konkreten Werte (s.o.) gibt die Normalengleichung der Tangentialebene \(E\)$$E:\quad \begin{pmatrix}1\\ -2\\ 1\end{pmatrix} \vec x = -1$$Im folgenden habe ich versucht, das in Geoknecht3D darzustellen. Dort ist die (grüne) Ebene \(E\) mit ihrem Normalvektor gezeichnet. Die Z-Achse ist hier nicht gestaucht!
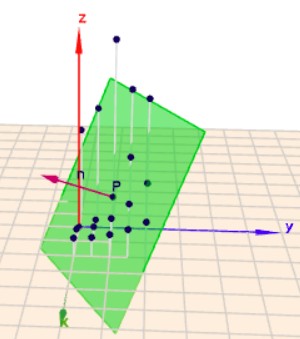
Die Punkte liegen in der Oberfläche der Funktion in der Umgebung von \(P(0|\,1)\). Klick auf das Bild, dann kannst Du es mit der Maus rotieren und Du bekommst einen besseren räumlichen Eindruck.
Oder in einem größeren Ausschnitt mit Wolfram Alpha.
Gruß Werner