Aufgabe:
Hallo wie kommt er in Aufgabe 7 zum V=440,8
und O=966,4?
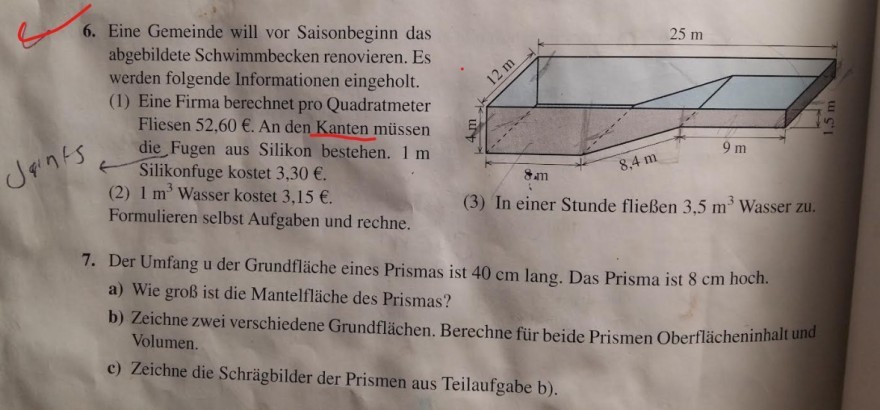
6. Eine Gemeinde will vor Saisonbeginn das abgebildete Schwimmbecken renovieren. Es werden folgende Informationen eingeholt.
(1) Eine Firma berechnet pro Quadratmeter
Fliesen \( 52,60 € \). An den Kanten müssen
die,Fugen aus Silikon bestehen. \( 1 \mathrm{~m} \)
Silikonfuge kostet \( 3,30 € \).
(2) \( 1 \mathrm{~m}^{3} \) Wasser kostet \( 3,15 € \).
Formulieren selbst Aufgaben und rechne.
(3) In einer Stunde fließen \( 3,5 \mathrm{~m}^{3} \) Wasser zu.
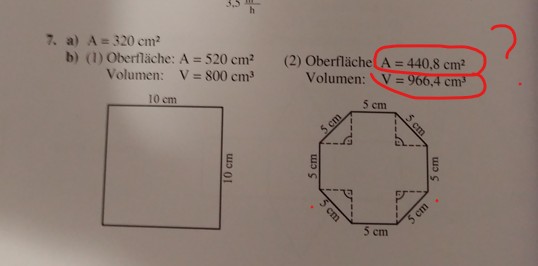
7. Der Umfang u der Grundfläche eines Prismas ist \( 40 \mathrm{~cm} \) lang. Das Prisma ist \( 8 \mathrm{~cm} \) hoch.
a) Wie groß ist die Mantelfläche des Prismas?
b) Zeichne zwei verschiedene Grundflächen. Berechne für beide Prismen Oberflächeninhalt und Volumen.
c) Zeichne die Schrägbilder der Prismen aus Teilaufgabe b).
Hallo , wei kommt er zu V und O ?
Oberfläche ist
O = 2 G+ M--( U * h)
O = 2* 120,7 + 40 *8
O=etw 561 cm^2 !! aber nicht 440,8 cm^2!!!
Voulmen = AG * h
V= 120,7 * 8 =965,6 cm^3 also wie fast im Buch --->966,4
Aber Oberfläche stimmt!
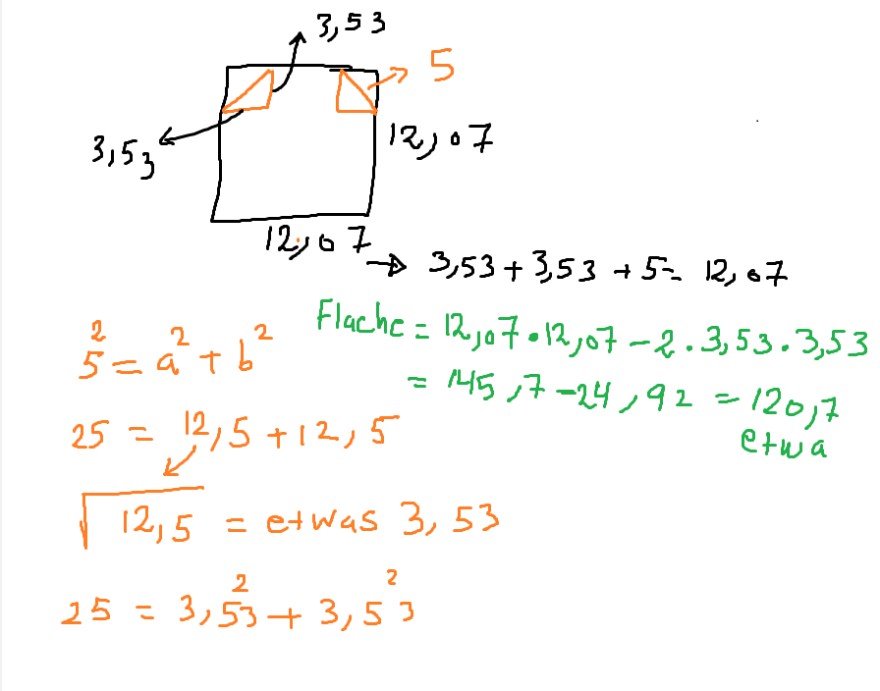
Text erkannt:
\( 3,53^{3} \prod \limits_{12, j 07}^{3,53} \rightarrow 3,53+3,53+5=12,07 \)
\( 5^{2}=a^{2}+b^{2} \) Flache \( =12,07 \cdot 12,07-2 \cdot 3,53 \cdot 3,53 \)
\( 25=12,5+12,5^{2} \)
\( \sqrt{12,5}= \) etwas 3,53
\( 25=3,5^{2}+3,5^{2} 3 \)