Aufgabe: Ist a ↘ 0 und ist b monoton fallend, nichtnegativ und gilt zusätzlich bn ≤ an füralle n ∈ N,
so gilt auch b ↘ 0.
Problem/Ansatz:
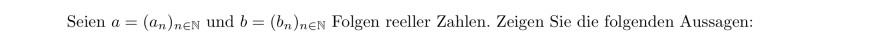
Text erkannt:
Seien \( a=\left(a_{n}\right)_{n \in \mathbb{N}} \) und \( b=\left(b_{n}\right)_{n \in \mathbb{N}} \) Folgen reeller Zahlen. Zeigen Sie die folgenden Aussagen:

Text erkannt:
(ii) Ist \( a \searrow 0 \) und ist \( b \) monoton fallend, nichtnegativ und gilt zusätzlich \( b_{n} \leq a_{n} \) für alle \( n \in \mathbb{N} \), so gilt auch \( b \searrow 0 \).