Hallo,
im Raum kannst Du eine Gerade nicht in Koordinatenform mit einer einzigen Gleichung darstellen. Hier benötigt man zwei Gleichungen.
Mein Ansatz war:
x1 = 1-2t
x2 = 2+2t
x3 = 4+t
richtig - und nun eliminiert man das \(t\), indem man eine der Gleichungen nach \(t\) auflöst und in die anderen einsetzt. $$x_3 = 4+t \implies t = x_3 - 4$$Einsetzen in die beiden anderen$$x_1 = 1 - 2x_3+8 \\ x_2 = 2 + 2x_3 - 8$$und ein wenig sortieren:$$x_1 + 2x_3 = 9 \\ x_2 - 2x_3 = -6$$Das Ergebnis ist aber nicht eindeutig! Es kommt z.B. darauf an, welche der drei Gleichungen man nach \(t\) auflöst. D.h. das Ergebnis aus dem Lösungsbuch kann davon abweichen!
Graphisch sieht das so aus:
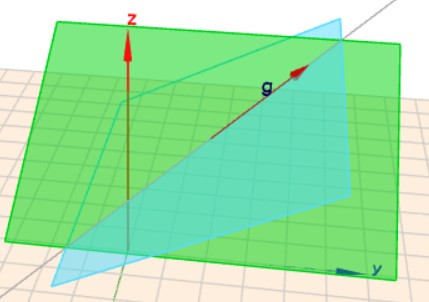
Jede der beiden Gleichungen beschreibt eine der skizzierten Ebenen. Und die Schnittgerade der Ebenen ist die Gerade \(g\). D.h. nur ein Punkt, der beide Gleichungen erfüllt, liegt auch auf \(g\).
Gruß Werner