Elementare Ableitungsregeln - bestimmen Sie die Steigung m usw...

Question

Aufgabe:

Untersuchen Sie, an welcher Stelle die Funktion f die Steigung m hat.

a) f(x) = 4/x, m = - 1/9

b) f(x) = 4/x^3, m = -0,75

Problem/Ansatz:

Wie geht das...

Comments

Du sollst nicht die Steigung m bestimmen (Titel), sondern bestimmen, an welcher Stelle die Funktion die Steigung m hat (Aufgabe). Also die Stellen x bestimmen.

Wie es geht, hast Du in den Titel geschrieben: Mit Ableiten. Die Ableitung ist die Steigung.

---

1/x = x^-1

1/x^3 = x^-3

Damit kannst du leicht ableiten.

Answer 1

Setze f ' (x) = m und berechne die möglichen

Werte von x, etwa so bei der ersten

f ' (x)= -4/x^2  also -4/x^2 = -1/9

                        <=>    36 = x^2

                         <=>  x=6 oder x=-6

f hat an 2 Stellen, nämlich bei 6 und bei -6 die Steigung -1/9.

Answer 2

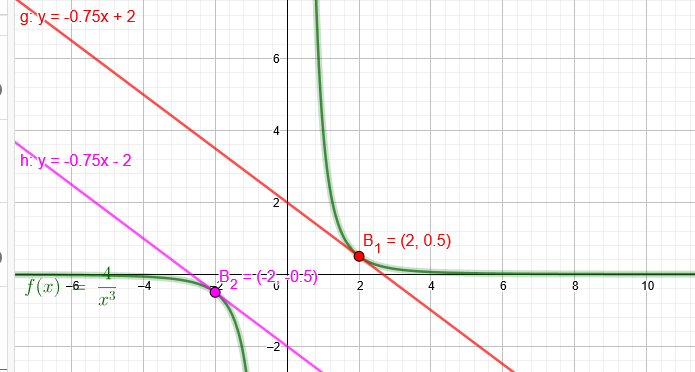
b)

f(x) = \( \frac{4}{x^3} \) , m = -0,75=-\( \frac{3}{4} \)

\( \frac{df(x)}{dx} \)=\( \frac{0*x^3- 4*3x^2}{(x^3)^2} \)=-\( \frac{12x^2}{x^6} \) =-\( \frac{12}{x^4} \)

-\( \frac{3}{4} \)=-\( \frac{12}{x^4} \)

\( \frac{1}{4} \)=\( \frac{4}{x^4} \)

\( x^{4} \)=16 |\( \sqrt[4]{} \)

x₁=2

x₂=-2

(x₃=2i)

(x₄=-2i)

Die letzten beiden Lösungen kommen nicht in Betracht.  

f(2)=\( \frac{1}{2} \)

f(-2)=-\( \frac{1}{2} \)