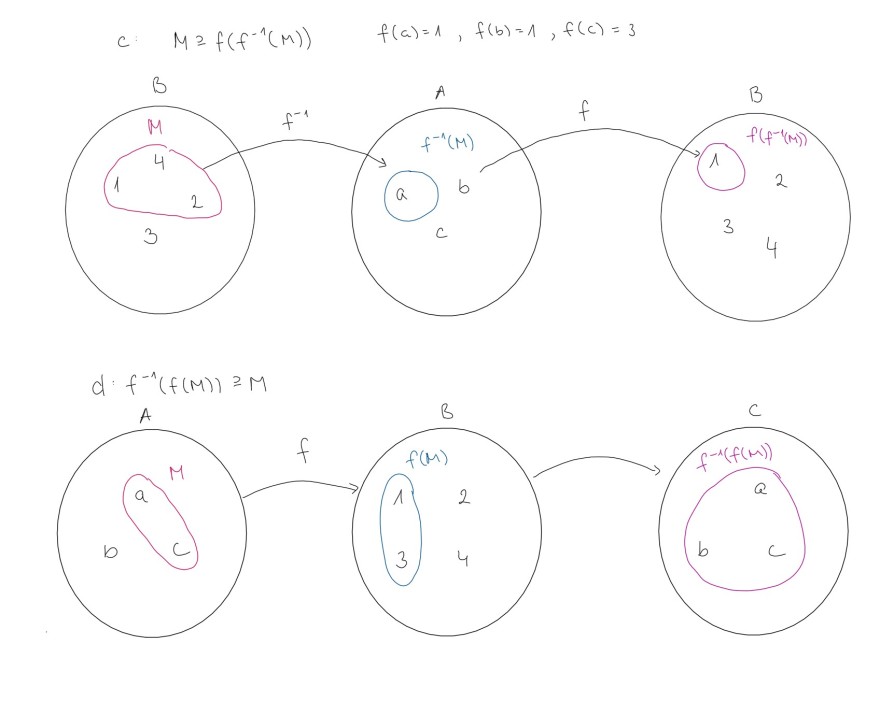
Zur Teilaufgabe c):
Betrachte erstmal das Urbild von M. Das sind alle Elemente aus dem Definitionsbereich von f die auf ein Element aus M abgebildet werden. Wendet man auf diese Elemente f an, so bekommt man eine Teilmenge von M heraus. (Es könnte sein, dass ein Element aus M nicht getroffen wird, da f nicht auf alle Elemente aus B bzw. M abbilden muss.) Falls f surjektiv ist, so gilt Gleichheit.
Zur Teilaufgabe d):
M ist nun eine Teilmenge von A. Wir betrachten die Bildpunkte von A unter der Abbildung f und nennen diese Menge f(M). Nun betrachten wir das Urbild von f(M). Natürlich müssen die Elemente aus M im Urbild liegen, da diese ja auf f(M) abgebildet werden. Daher gilt die Inklusion. Es könnte aber sein, dass andere Elemente aus A auch auf Elemente aus f(M) abgebildet werden. Diese kommen dann bei der Betrachtung des Urbildes noch dazu. Gleichheit würde gelten wenn f Injektiv ist.
Das ist vielleicht ein bisschen kompliziert, aber vielleicht hilft dir die Grafik s.u.
Text erkannt: