Aufgabe:
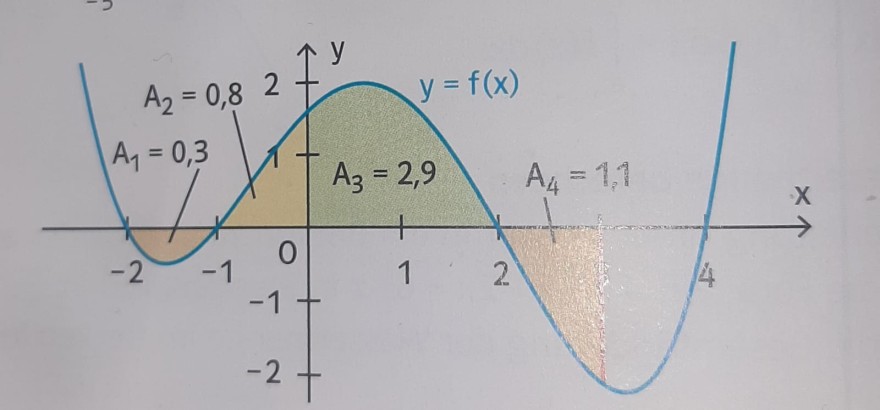
Bestimmen Sie das Integral mithilfe der angegbenen Flächeninhalte.
a) \( \int\limits_{-2}^{ 0} \) f(x) dx
b) \( \int\limits_{-1}^{2} \) f(x) dx
c) \( \int\limits_{0}^{ 3} \) f(x) dx
d) \( \int\limits_{-2}^{ 3} \) f(x) dx
Problem/Ansatz:
a) 0,5
b) 3,7
c) 1,8
d) 3,4
----
Anmerkung von MontyPython:
Das Original sah so aus:
Aufgabe: Bestimmen Sie das Integral mithilfe der angegbenen Flächeninhalte. a) \( \int\limits_{0}^{\infty -2} \) f(x) dx b) \( \int\limits_{2}^{\infty -1} \) f(x) dx c) \( \int\limits_{3}^{\infty 0} \) f(x) dx d) \( \int\limits_{3}^{\infty -2} \) f(x) dx Hinweis: Die Unendlichkeitszeichen müssen weg, aber dann verfällt das Integralzeichen, wenn ich das so tue, Problem/Ansatz: a) 0,5 b) 3,7 c) 1,8 d) 3,4