Welches Volumen hat es?

Question

Aufgabe:

Aufgabe 40: In einer Gussform mit quadratischer Oberfläche befinden sich als Hohlraum zwei aneinander gefügte Viertelkreis-Segmente mit einem Radius von r = 15 cm. Der Hohlraum hat eine Höhe von 10 cm. Welches Volumen hat es?

Problem/Ansatz:

Wie berechne hier das Volumen?

https://mathe.aufgabenfuchs.de/koerper/zylinder.shtml

Answer 1

V = (1/4·pi·r^2 + 1/4·pi·r^2 - r^2)·h

V = (1/4·pi·15^2 + 1/4·pi·15^2 - 15^2)·10 = 1284.3 cm³

Comments

Die Formel danke!

Answer 2

Der gelbe Hohlraum mit der Kreisgleichung:

\(V = 4 \cdot \int \limits_{0}^{\frac{15 \sqrt{2}}{2}}\left(\sqrt{15^{2}-x^{2}}-\frac{15 \sqrt{2}}{2}\right) d x\cdot 10 = 1125 π - 2250 ≈ 1284,3 \)

wobei ich als Grundfläche viermal die grüne Fläche genommen habe:

Answer 3

Hallo,

den Flächeninhalt einer Linse in einem Quadrat kannst du mit der Formel

\(A=(\frac{1}{2}\pi-1)\cdot r^2\)

berechnen.

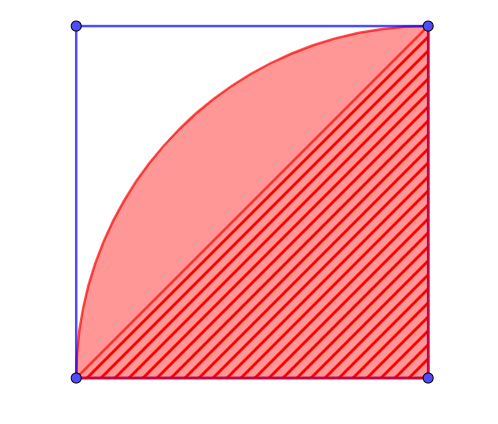
Die Fläche des Viertelkreises ist \(A_{Viertelkreis}=\frac{1}{4}\pi\cdot r^2\).

Die des (schraffierten) Dreiecks \(A_{Dreieck}=\frac{1}{2}r^2\).

Damit ergibt sich für die halbe Linse \(A_{hL}=\frac{1}{4}\pi\cdot r^2-\frac{1}{2}r^2\) und für die ganze \(A_{Linse}=2\cdot\bigg(\frac{1}{4}\pi\cdot r^2-\frac{1}{2}r^2\bigg)=\frac{1}{2}\pi r^2-r^2=r^2\cdot\bigg(\frac{1}{2}\pi-1\bigg)\)

Multipliziere dein Ergebnis dann noch mit der Höhe.

Gruß, Silvia