Hallo,
gegeben ist also die Funktion \(f(x)=x^3\) und der Flächeninhalt im Intervall von 1 bis 5 soll annähernd durch die Ober- bzw. Untersumme bestimmt werden.
Wenn du das Intervall in vier gleich große Rechtecke unterteilst, sieht die "Treppe" für die Obersumme ("Ober", weil die Summe größer als das gesuchte Flächeninhalt ist) so aus:
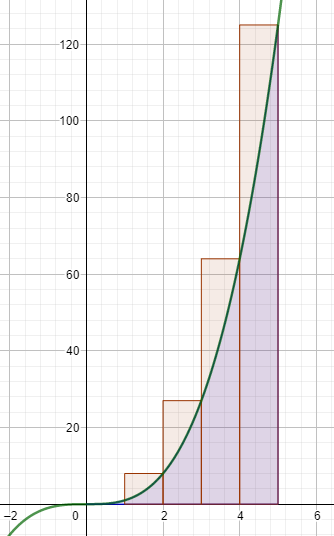
Die Breite jedes Rechtecks ist 4 : 4 = 1
Diese Breite verringert sich mit der Anzahl der Rechtecke. Bei der Unteilung in 8 Rechtecke beträgt die Breite nur noch 4 : 8 = 0,5
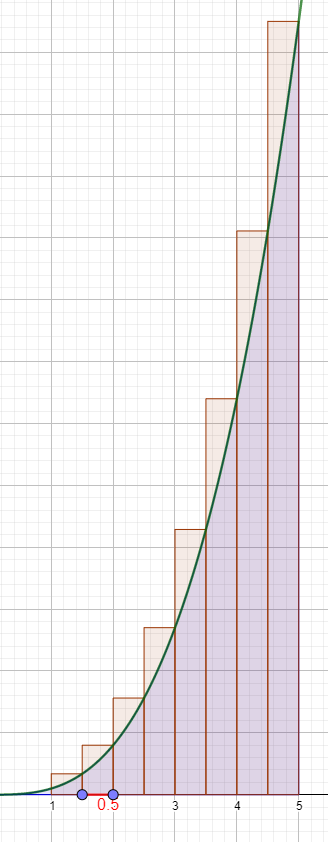
Die Höhe der Rechtecke entspricht den Funktionswerten an den Teilpunkten.
Die Obersumme kann also dargestellt werden als
\(0,5\cdot1,5^3+0,5\cdot2^3+0,5\cdot2,5^3+0,5\cdot3^3+0,5\cdot3,5^3+0,5\cdot4^3+0,5\cdot4,5^3+0,5\cdot5^3=188,5\)
oder alternativ
\(0,5\cdot\bigg(\frac{3}{2}\bigg)^3+0,5\cdot\bigg(\frac{4}{2}\bigg)^3+0,5\cdot\bigg(\frac{5}{2}\bigg)^3+0,5\cdot\bigg(\frac{6}{2}\bigg)^3+0,5\cdot\bigg(\frac{7}{2}\bigg)^3+0,5\cdot\bigg(\frac{8}{2}\bigg)^3+0,5\cdot\bigg(\frac{9}{2}\bigg)^3+0,5\cdot\bigg(\frac{10}{2}\bigg)^3=188,5\)
Je höher die Anzahl der Streifen, desto größer die Annäherung.
Gruß, Silvia