Hallo Zahri,
ich möchte NUR wissen ,wie ich solche Textaufgabe gut versehen kann
Textaufgaben sind naturgemäß die Aufgaben wo sich Schüler am schwersten tun. Da bist Du nicht alleine. Übung und Geduld und beständiges Nachfragen können da weiter helfen.
Mal ganz langsam an den Satz herangehen:
Untersuche, ...
heißt: Das ist eine Aufforderung etwas zu tun. Und zwar einen Sachverhalt näher zu betrachten, zu 'untersuchen' und Dir eben darüber Gedanken machen.
Untersuche, ob der Umkreis ...
Ok - es geht um den Umkreis. Und weiter wird hier vorweg genommen, dass es um den Umkreis eines Dreiecks geht, weil das Wort 'Dreieck' später im gleichen Satz wieder auftaucht. Der 'Umkreis' ist der eine(!) Kreis, der durch alle Eckpunkte eines Dreiecks läuft (so wie auf dem Bild in Deiner Frage)
Also sollst Du irgendwas am Umkreis eines Dreiecks untersuchen.
Untersuche, ob der Umkreis der kleinste Kreis ist, ....
Impliziert wird hier die Frage: Ist der Umkreis der kleinste Kreis? Nur, wenn etwas das kleinste sein soll, dann muss es ja mehr als einen geben! Und dann wird's auch schon mathematisch. Das bedeutet: Solange nichts eingeschränkt ist, ist ALLES erlaubt. Es sind ALLE erdenklichen Kreise gemeint. Hier eine kleine Auswahl:
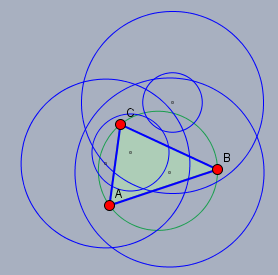
Ist der Umkreis (grün) der kleinsten Kreis von allen?
Untersuche, ob der Umkreis der kleinste Kreis ist, der das Dreieck enthält.
Nein - es gibt sicher kleinere Kreise. Und hier kommt die Einschränkung: Es werden nur die Kreise angeschaut, die das Dreieck enthalten. Was bedeutet 'enthalten'? Das ist wie ein dreieckiger Keks, der in einer kreisrunden Keksdose liegt. Wenn der Keks in die Dose passt, ohne eine Ecke abzubrechen, bildet die Dose einen (von vielen) möglichen Kreis, der das Dreieck (den Keks) enthält.
Gruß Werner