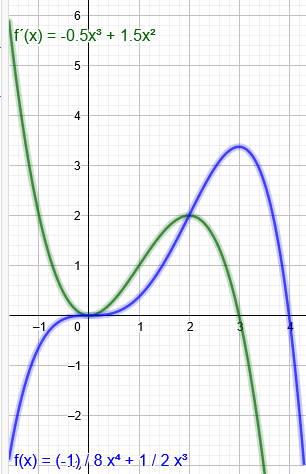
f´(x)=a*x^2*(x-3)
P(2|2)
f´(x)=4a*(2-3)=-4a -4a=2 a=-0,5
f´(x)=-0,5 *x^2*(x-3)=-0,5x^3+1,5x^2
f(x)=\( \int\limits_{}^{} \)(-0,5x^3+1,5x^2)*dx=-0,125x^4+0,5x^3+C
rote Aussagen sind falsch grüne Aussagen sind richtig
… auf dem Intervall (1.5,2.5) eine Extremstelle
… auf dem Intervall (2,4) eine Extremstelle
… auf dem Intervall (–1,0) keine Extremstelle
… auf dem Intervall (-1,4) zwei Extremstellen
"Ich weiß, dass bei der f‘(x) die Nullstellen bei f(x) dann eine Extremstellen sind oder?"
Bei N(3|0) liegt eine einfache Nullstelle vor , darum Extremwert bei f(x)
"Wieso ist dann die letzte Aussage nicht richtig obwohl es zwei Nullstellen hat?"
Bei N(0|0) ist eine doppelte Nullstelle, darum ist bei f(x) dort ein Sattelpunkt und keine Extremstelle.
Zur Verdeutlichung beide Funktionen im Bild: