Tangentensteigung von Ableitung mit cos berechnen

Question

Aufgabe:

Untersuchen Sie, ob der Graph von f mit f(x) = 1,5 sin(2x) im Intervall [0, π/2] eine Tangente mit der Steigung -3 besitzt.

Problem/Ansatz:

Hi, bei -3 = 3 cos(2x) hänge ich fest. Wie berechnet man das? Ist das überhaupt der richtige Weg, um diese Aufgabe zu lösen?

Vielen Dank und LG

Answer 1

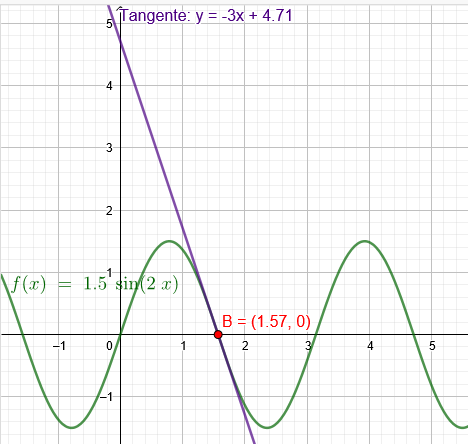
-3 = 3 cos(2x)

cos(2x)=-1      cos(2x)=\( cos^{2} \)x-\( sin^{2} \)x    \( cos^{2} \)x=1- \( sin^{2} \)x

cos(2x)=1-2\( sin^{2} \)x

-1=1-2\( sin^{2} \)x    1=\( sin^{2} \)x  |\( \sqrt{} \)

1.)sin(x)=1         x=\( \frac{π}{2} \)

2.)sin(x)=-1    x=-\( \frac{π}{2} \)  liegt nicht im Intervall  [0, \( \frac{π}{2} \)]

Answer 2

        -3 = 3 cos(2x)

<=>   -1 = cos(2x)

<=>  -1 = cos(2x)

<=>   pi = 2x

<=>   pi/2 = x

Answer 3

-3 = 3 cos(2x) 
-1 = cos(2x)  | arcos
arcos(2x) = arccos(-1)
2x = 180 °
x = 90 °