Höhenlinie einer Radweg-Überführung

Question

Aufgabe:

Bestimmen Sie die Höhenlinie einer Radweg-Überführung

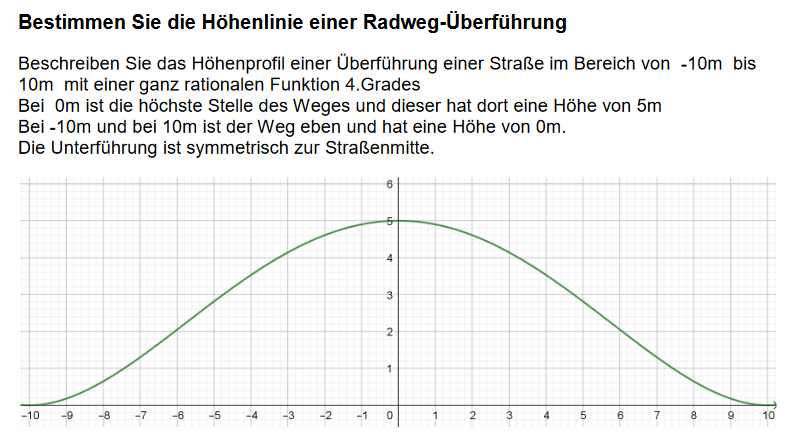
Beschreiben Sie das Höhenprofil einer Überführung einer Straße im Bereich von $-10 \mathrm{~m}$ bis $10 \mathrm{~m}$ mit einer ganz rationalen Funktion 4.Grades

Bei $0 \mathrm{~m}$ ist die höchste Stelle des Weges und dieser hat dort eine Höhe von $5 \mathrm{~m}$ Bei $-10 \mathrm{~m}$ und bei $10 \mathrm{~m}$ ist der Weg eben und hat eine Höhe von 0 m.

Die Unterführung ist symmetrisch zur Straßenmitte.

Problem/Ansatz:

Ich beschäftige mich aktuell mit der oben abgebildeten Steckbriefaufgabe, bei welcher ich zu keinem Ergebnis bisher gekommen bin.

Was ich soweit aufgestellt habe:

Ganzrationale Funktion 4. Grades bei Symmetrie:

f(x) = ax⁴ + bx² + c
f'(x) = 4ax³ + 2bx
f''(x) = 12ax² + 2b

Und folgende Informationen habe ich aus der Aufgabenstellung extrahiert:

f(0) = 5 (Nullstelle) und zugleich
f'(0) = 0 (Höchstpunkt)
f(10) und f(-10) = 0

Wenn ich f'(0) = 0 auflöse, ergibt sich eine Identität (0 = 0) ohne das eine Variable erhalten bleibt.
f(0) = 5 eingesetzt ergibt c = 5

Und somit verbleiben lediglich f(10) und f(-10) die ich nicht gegeneinander verrechnen kann, da sich sonst ebenfalls 0 = 0 ergibt.

Hat hier jemand eine Idee?

Answer 1

Du hast f'(10)=0 vergessen.

Answer 2

Alternativweg über die Nullstellenform der Parabel 4.Grades:

f(x)=a*(x+10)²*(x-10)²   Extremwerte bei x=-10 und bei x=10

P(0|5)

f(0)=a*(0+10)²*(0-10)²=10000a

10000a=5      a=$\frac{5}{10000}$

f(x)=$\frac{5}{10000}$*(x+10)^2*(x-10)^2

Answer 3

Wegen Symmetrie zur y-Achse
f ( x ) = a * x⁴ + b * x² + c
f ´( x ) = 4ax³ + 2bx

f(0) = 5 (Nullstelle) und zugleich
f'(0) = 0 (Höchstpunkt)
f(10) = 0
f(-10) = 0

und

f ´ (10) = 0
f ´ (-10) = 0

f(x) = 0,0005·x⁴ - 0,1·x² + 5