Korrelationskoeffizient nach Pearson Wie im Taschenrechener eingeben ohne das Fehler kommt?

Question

Aufgabe:

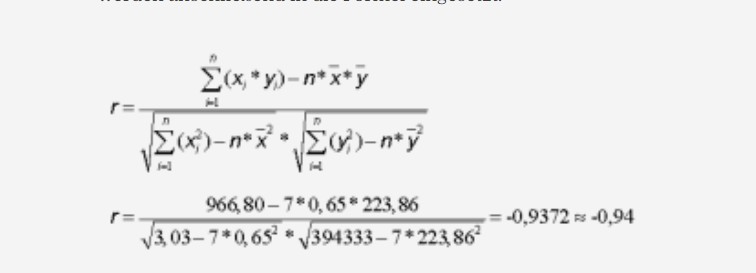
Text erkannt:

\( \begin{aligned} r &=\frac{\sum \limits_{i=1}^{n}\left(x_{j} * y_{i}\right)-n^{*} \bar{x}^{*} \bar{y}}{\sqrt{\sum \limits_{i=1}^{n}\left(x_{j}^{2}\right)-n^{*} \bar{x}^{2}}=\sqrt{\sum \limits_{i=1}^{n}\left(y_{j}^{2}\right)-n^{*} \bar{y}^{2}}} \\ r &=\frac{966,80-7 * 0,65 * 223,86}{\sqrt{3,03-7 * 0,65^{2}} * \sqrt{394333-7 * 223,86^{2}}}=-0,9372 \approx=0,94 \end{aligned} \)

Text erkannt:

b) Um das Bestimmtheitsmaß zu berechnen, ermittelt man der Els zunächst den Korrelationskoeffizienten nach Bravais-Pearson:
\( r_{x y}=\frac{3822,74-8 \cdot 106,20 \cdot 4,175}{\sqrt{5.821,69-8 \cdot 106,20^{2}} \sqrt{154,16-8 \cdot 4,175^{2}}}=0,59 . \)

Problem/Ansatz:

Wie gebe ich dieses Ergebniss im Taschenrechner ein ich weiß das man aus der Wurzel mit negativern Zahlen nicht rechnen kann aber wie kann ich das einegeb ohne das die ganze zeit ein Fehler im Taschenrechner kommt?

Danke für eure Hilfe

Answer 1

Hallo

deine Formel ist falsch! das \( \sqrt{x_j^2-n\cdot \bar(x)^2} \) ist falsch

richtig ist \( \sqrt{\sum\limits_{j=0}^{n}{x_j^2}}  -n\cdot \bar{x} \)

Gruß lul

Comments

Ja mir geht es aber nicht darum sondern wie ich es in den Taschenrechner eingeben kann mit negativen wurzel also mit der oberen formel

---

Hm,

welche Formel? siehst Du was, was ich nicht sehe?

Merkwürdiger TR mit Dezimalkomma und Tausendertrennung?

@G:Das Ergebnis r ist zweimal falsch: r=-0.9213

Ergebnisse gibt man auch nicht ein, man ließt sie ab ;-)

und meinem Formelbuch lese ich

Bravais-Pearson

\(\large r=\frac{\sum\limits_{k=1}^{n}(x_k-\overline x)(y_k-\overline y)}{\sqrt {\sum\limits_{k=1}^n(x_k-\overline x)^2 \sum\limits_{k=1}^n(y_k-\overline y)^2}} \)

Add: es darf keine negative Wurzel bei diesem Sachverhalt entstehen - sieht man auch an meiner Formel!