DGL Grenzwert bestimmen

Question

Aufgabe:

Gegen welchen \( y \)-Wert konvergiert die Lösung der DGL: \( y^{\prime}(x)=16-y^{2} \) mit dem Anfangswert \( y(0)=6 \) begrenzt wird!

Lösung:

\( \lim \limits_{x \rightarrow \infty} y(x)=4 \)

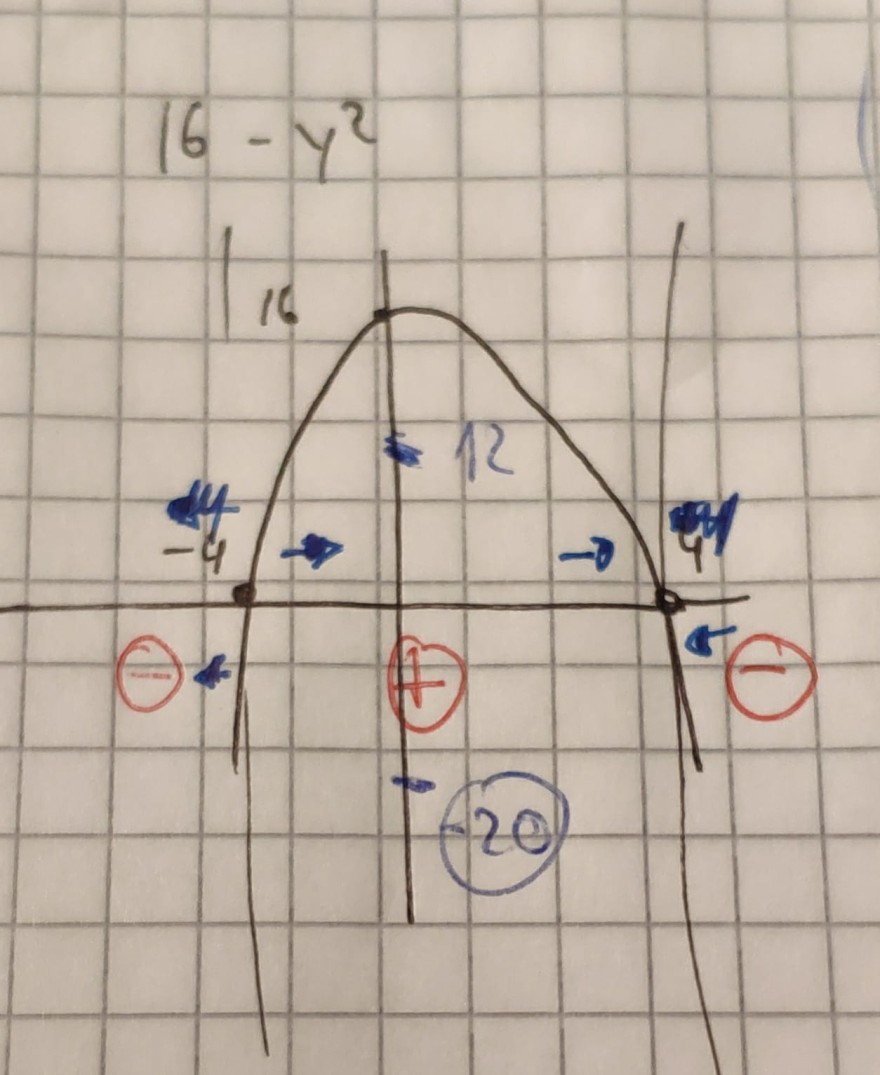
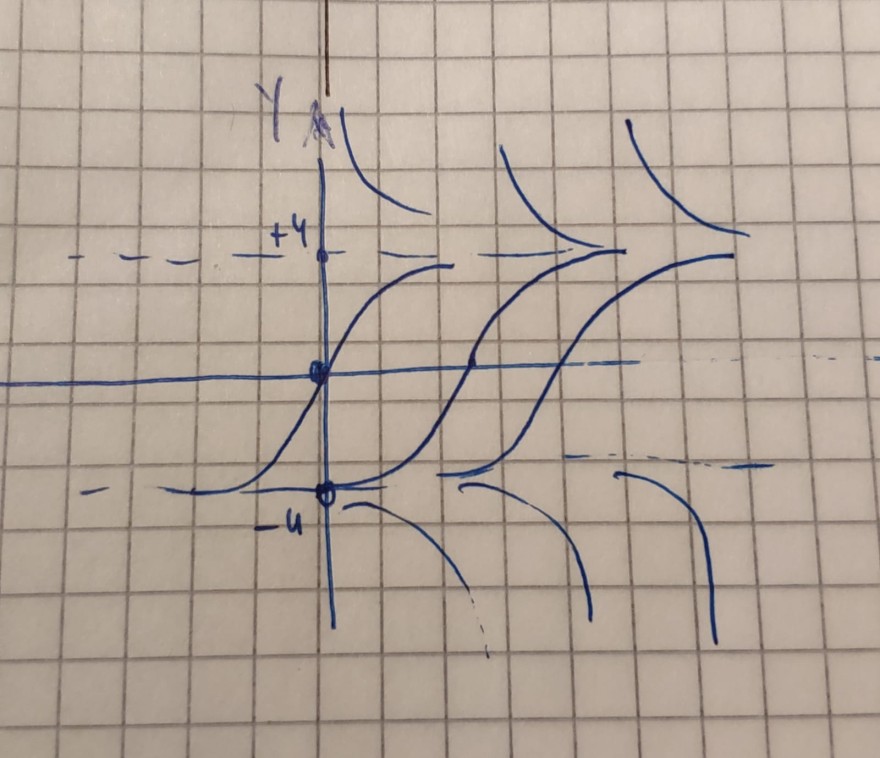
Frage zum Verständnis: Ich verstehe bei der Aufgabe nicht, wie man sich das bildlich vorstellen kann? Ich habe mir einmal die f(y) über y Funktion aufgezeichnet (Parabel) und die dazugehörige y-x Funktion (Isoklinen). Wenn ich den Anfangswert von y(0)=6 bei y´einsetze, erhalte ich für y´= - 20. Aber eine Annäherung kann ich da nicht erkennen. Also klar, bei den Isoklinenbild kann man die die Annäherung zu 4 und - 4 deutlich erkennen. Ich verstehe aber nicht, wie ich mit diesem Anfangswert umzugehen habe.

Gibt es denn einen Anfangswert, bei dem die Funktion gegen unendlich geht? Wenn ja, wo ist die Grenze?

Comments

Ich verstehe die Aufgabe so, dass Du das Anfangswert Problem lösen sollst Stichwort: Getrennte Verändrrliche

Answer 1

Hallo,

Wenn ich den Anfangswert von y(0)=6 bei y´ einsetze, erhalte ich für y´= - 20.

Das ist leider falsch, der Anfangswert wird in die Lösung eingsetzt.

Die Lösung erfolgt via " Trennung der Variablen"

y'= 16-y^2 

dy/dx= 16-y^2

dy/(16-y^2)=dx

usw.

Lösung:

\( y(x)=\frac{4\left(5 e^{8 x}+1\right)}{5 e^{8 x}-1} \)

Wenn Du dann von der Lösung den Grenzwert bildet, kommt 4 heraus.