Aufgabe:
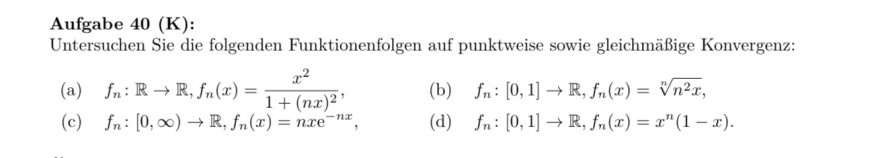
Text erkannt:
Aufgabe \( 40(\mathrm{~K}): \)
Untersuchen Sie die folgenden Funktionenfolgen auf punktweise sowie gleichmäßige Konvergenz:
(a) \( f_{n}: \mathbb{R} \rightarrow \mathbb{R}, f_{n}(x)=\frac{x^{2}}{1+(n x)^{2}} \),
(b) \( f_{n}:[0,1] \rightarrow \mathbb{R}, f_{n}(x)=\sqrt[n]{n^{2} x} \),
(c) \( f_{n}:[0, \infty) \rightarrow \mathbb{R}, f_{n}(x)=n x \mathrm{e}^{-n x} \),
(d) \( f_{n}:[0,1] \rightarrow \mathbb{R}, f_{n}(x)=x^{n}(1-x) . \)
Problem/Ansatz:
Wie soll man da rangehen??