Hallo,
zeichne eine beliebige Gerade g (grün) und die zwei Punkte A und B auf eine Seite der Geraden, hier unterhalb.
Zeichne einen Halbkreis (Thaleskreis) über der Strecke AB. Wenn der Abstand von A und B zum Mittelpunkt M der Strecke kleiner ist als der Abstand von M zu der Geraden, kannst du C nicht konstruieren, so dass die Bedingung "rechter Winkel" erfüllt ist.
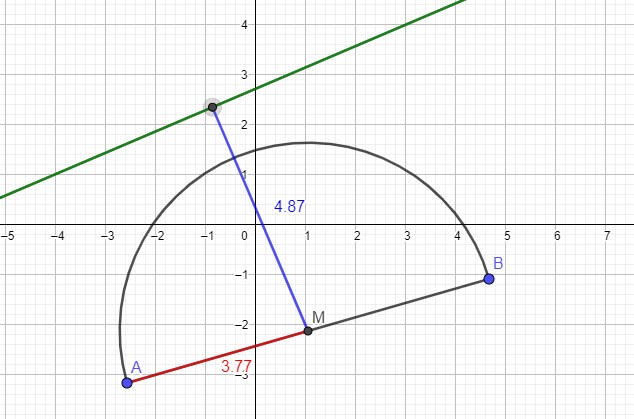
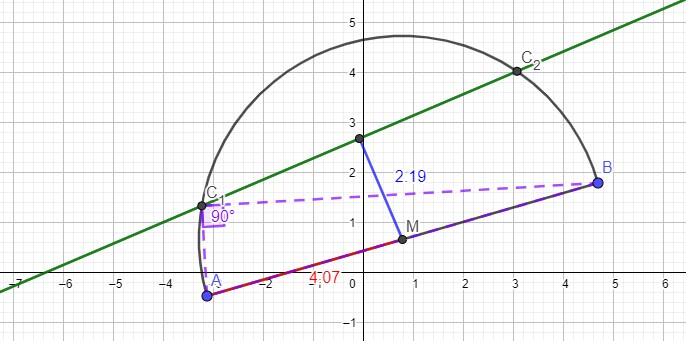
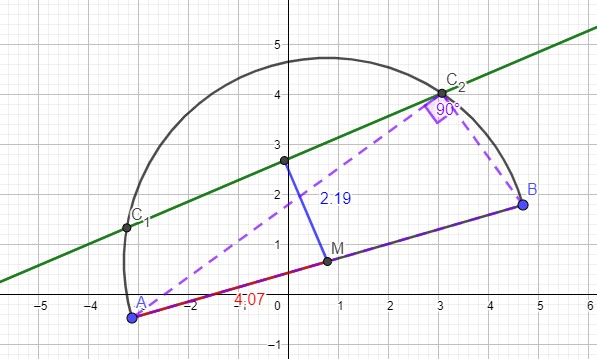
Wenn der Abstand AM größer ist als der Abstand gM, dann schneidet der Thaleskreis die Gerade in zwei Punkten, die die Bedingung erfüllen.
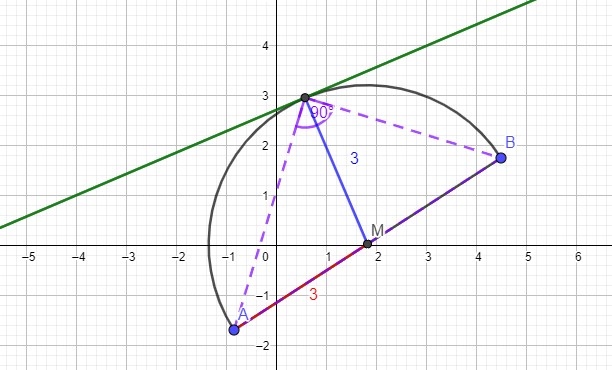
Ist der Abstand AM genau so groß wie der Abstand gM, dann gibt es einen Punkt C, der die Bedingung erfüllt.
Gruß, Silvia