Bestimmen sie die erste und zweite Ableitung der Funktion f und untersuchen sie f auf Extremstellen

Question

Aufgabe:

3 Destimmen Sie die erste und die zweite Ableitung der Funktion \( f \) und untersuchen Sie f auf Extremstellen.
f) \( f(x)=x^{2} \cdot e^{x} \)

Problem/Ansatz:

Ich verstehe nicht genau was die 2. Ableitung ist und wie ich die notwendige und hinreichende Bedingung hier berechne bzw. was das Ergebnis ist.

Könnte mir vlt die Aufgabe jemand vorrechnen, weil ich die meisten Sachen am besten durch eine Lösung verstehe :)

Answer 1

Klartext meiner Aufgabe:

Titel: Bestimme die erste und die zweite Ableitung der Funktion f und untersuchen Sie f auf Extremstellen.

Stichworte: exponentialfunktion,funktion,ableitungen,produktregel

Aufgabe:

Bestimmen Sie die erste und die zweite Ableitung der Funktion f und untersuchen Sie f auf Extremstellen.

f) f(x)=x^2×e^x
Problem/Ansatz:

Ich weiß nicht wie ich die Ableitungen berechnen und bei e-Funktionen auf Extremstellen untersuchen soll. Wäre super, wenn es mir jemand erklären kann. Dankr im voraus!

Answer 2

f) f(x)=x²×e^x

Das ist ein Produkt.

Also berechnet man die Ableitung mit der Produktregel

        \(f(x) = g(x)\times h(x) \implies f'(x) = g(x)\times h'(x) + g'(x)\times h(x)\).

Extremstellen sucht man genau so wie bei anderen Funktionen:

1. Nullstellen der Ableitung bestimmen
2. Mit der zweiten Ableitung bestimmen ob es sich um Hochpunkte oder Teifpunkte handelt.
   

Answer 3

Hallo

1. f(x) nach der Produktregel differenzieren, Extrema bei f'(x)=0 (e^x ausklammern, das ist immer ungleich 0 ) du findest die 2 Nullstellen  bei x1=0 und x2=-2

f'(x) ist die Funktion, die du ableiten musst, das gibt die 2 te Ableitung also f''(x)=(f'(x))'

in f''(x1)einsetzen : wenn f''>0 ist bei x1 ein Minimum. wenn f''<0 ein Max Wenn =0 ein Sattelpunkt.  entsprechend f''(x2)

Das differenzieren musst du zum Üben schon selbst machen. Zur Kontrolle kannst du dir die Funktion ja plotten lassen.

Gruß lul

Answer 4

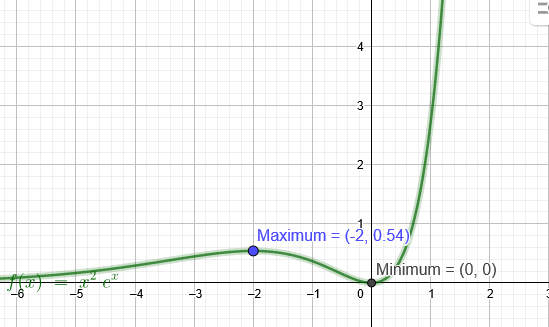
\( f(x)=x^{2} \cdot e^{x} \)

f´(x)=2x*\( e^{x} \)+\( x^{2} \) *\( e^{x} \)=\( e^{x} \)*(\( x^{2} \) +2x)

\( e^{x} \)*(\( x^{2} \) +2x)=0     \( e^{x} \) kann nicht 0 werden.

\( x^{2} \) +2x=0

x*(x+2)=0

x₁=0  \( f(0)=0^{2} \cdot e^{0} \)=0

x₂=-2  \( f(-2)=(-2)^{2} \cdot e^{-2} \)=\( \frac{4}{e^2} \)

Art der Extremwerte:

f´´(x)=\( e^{x} \)*(\( x^{2} \) +2x)+\( e^{x} \)*(2x+2)

f´´(0)=\( e^{0} \)*(\( 0^{2} \) +2*0)+\( e^{0} \)*(2*0+2)=2>0   Minimum

f´´(-2)=\( e^{-2} \)*(\( (-2)^{2} \) +2*(-2))+\( e^{-2} \)*(2*(-2)+2)=-\( \frac{2}{e^2} \)<0   Maximum