Grenzwerte von verschiedenen Funktionen berechnen

Question

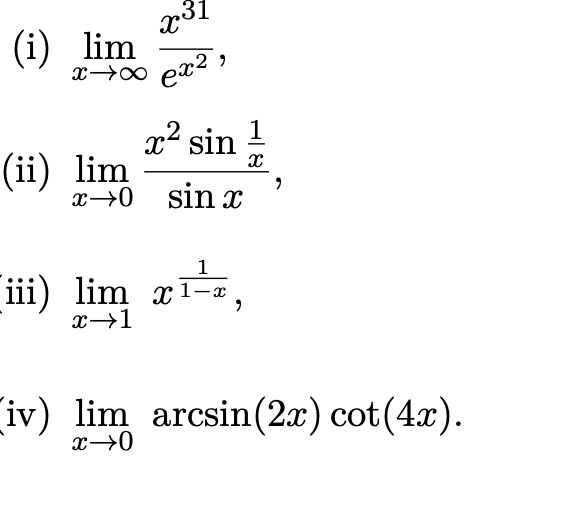
Text erkannt:

(i) \( \lim \limits_{x \rightarrow \infty} \frac{x^{31}}{e^{x^{2}}} \),
(ii) \( \lim \limits_{x \rightarrow 0} \frac{x^{2} \sin \frac{1}{x}}{\sin x} \),
iii) \( \lim \limits_{x \rightarrow 1} x^{\frac{1}{1-x}} \),
(iv) \( \lim \limits_{x \rightarrow 0} \arcsin (2 x) \cot (4 x) \)

Aufgabe:

…

Problem/Ansatz:

Comments

iii)

Verwende: x^(g(x) = e^(g(x)*lnx)

Answer 1

Mit L'Hospital:
\( \lim \limits_{x \rightarrow \infty} \frac{x^{31}}{e^{x^{2}}}=\lim \limits_{x \rightarrow \infty} \frac{31 x^{30}}{e^{x^{2}} \cdot 2 x}=\lim \limits_{x \rightarrow \infty} \frac{31 x^{29}}{2 e^{x^{2}}}=\lim \limits_{x \rightarrow \infty} \frac{31 \cdot 29 x^{28}}{2 \cdot 2 x \cdot e^{x^{2}}}=\lim \limits_{x \rightarrow \infty} \frac{31 \cdot 29 x^{27}}{2 \cdot 2 \cdot e^{x^{2}} \ldots} \)
Vielleicht kannst du da ein Gesetz herleiten.