Wie lang ist der kürzeste Weg (abhängig von a), auf dem dies möglich ist?

Question

Gegeben ist ein gerader Kreiskegel mit einer Mantellinie der Länge 2a und einem Grundkreisradius a/2. In einem Punkt P auf der Kegeloberfläche im Abstand a von der Kegelspitze startet ein Insekt um den Kegel einmal zu umrunden und nach P zurückzukehren. Wie lang ist der kürzeste Weg (abhängig von a), auf dem dies möglich ist?

Comments

ist a der Grundkreisradius? dann ist der Weg 4a

lul

---

Die Aufgabenstellung ist unvollständig. Bei einem sehr spitzen Kegel ist der Weg einer Umrundung sehr gering. Bei einem flachen Kegel mit gleicher Mantellinienlänge ist der Weg größer.

---

Aufgabe wurde ergänzt. Dank an lul und an abakus.

---

Ist P auf der Kegeloberfläche?

---

Ja, danke - noch eine Unvollständigkeit.

Answer 1

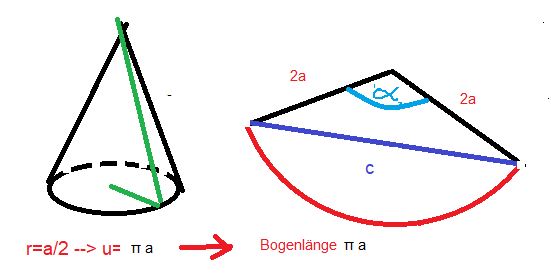
Ein Vollkreis mit dem Radius 2a hat den Umfang 4πa. Hat ein Kreisbogen mit dem gleichen Radius nur die Bogenlänge πa, so handelt es sich um einen Viertelkreis, und α in der rechten Abbildung (aufgeschnittener Kegelmantel) ist 90°.

Startet man eine Umrundung auf dem unteren Rand, denn stellt c die Länge des dafür kürzesten Weges dar. Mit α= 90°.gilt c=2√2a. Startet man nicht am unteren Rand, sondern auf halber Höhe, ist die minimale Weglänge c/2=√2a.