Wie kürze ich mit Wurzeln

Question

Hallo, ich habe meine Aufgabe und soll auf hochpunkte etc. untersuchen.

Ich würde aber gerne vorher meine Ableitung etwas vereinfachen aber die Wurzeln machen mir leider Schwierigkeiten..

Kann mir einer Tipps geben und mir weiterhelfen wie ich am besten mit solchen Wurzeln rechne bzw vereinfache?

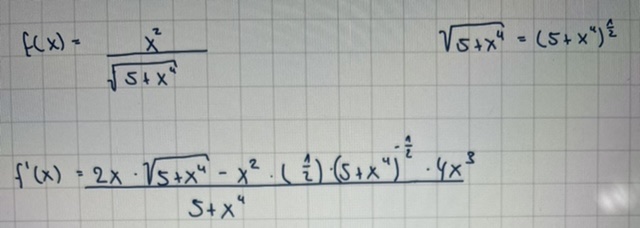
Text erkannt:

\( f(x)=\frac{x^{2}}{\sqrt{5+x^{4}}} \quad \sqrt{5+x^{4}}=\left(5+x^{4}\right)^{\frac{1}{2}} \)
\( f^{\prime}(x)=\frac{2 x \cdot \sqrt{5+x^{4}}-x^{2} \cdot\left(\frac{1}{2}\right) \cdot\left(5+x^{4}\right)^{-\frac{1}{2}} \cdot 4 x^{3}}{5+x^{4}} \)

Answer 1

Aloha :)

Du hast die erste Ableitung noch nicht vollständig zusammengefasst. Ich rechne dir das mal mit Hilfe von Produkt- und Kettenregel vor:$$f(x)=\frac{x^2}{\sqrt{5+x^4}}=\underbrace{x^2}_{=u}\cdot\underbrace{\left(5+x^4\right)^{-\frac12}}_{=v}$$$$f'(x)=\underbrace{2x}_{=u'}\cdot\underbrace{\left(5+x^4\right)^{-\frac12}}_{=v}+\underbrace{x^2}_{=u}\cdot\underbrace{\left(\overbrace{-\frac12\left(5+x^4\right)^{-\frac32}}^{\text{äußere Abl.}}\cdot\overbrace{4x^3}^{\text{innere Abl.}}\right)}_{=v'}$$Ja, das sieht schlimm aus, aber jetzt klammern wir \((5+x^4)^{-\frac32}\) aus:$$f'(x)=(5+x^4)^{-\frac32}\left(2x(5+x^4)-\frac12x^2\cdot4x^3\right)=(5+x^4)^{-\frac32}\left(10x+2x^5-2x^5\right)$$$$f'(x)=\frac{10x}{\left(5+x^4\right)^{\frac32}}$$

Die zweite Ableitung liefert einen ähnlich übersichtlichen Ausdruck:$$f''(x)=-\frac{50(x^4-1)}{\left(5+x^4\right)^{\frac52}}$$Kriegst du \(f''(x)\) alleine hin? Falls nicht, frag hier einfach nochmal nach.

Comments

Hallo:)

Danke für deine Antwort:)

Ich habe das echtbgut nachvollziehen können aber bei der 2. Ableitung komme ich schon wieder nicht weiter

---

Kein Problem, ich habe dir ja extra angeboten, dass du nochmal nachfragen kannst ;)

Machen wir die zweite Ableitung zusammen:$$f'(x)=\underbrace{10x}_{=u}\cdot\underbrace{(5+x^4)^{-\frac32}}_{=v}$$$$f''(x)=\underbrace{10}_{=u'}\cdot\underbrace{(5+x^4)^{-\frac32}}_{=v}+\underbrace{10x}_{=u}\cdot\underbrace{\overbrace{\left(-\frac32(5+x^4)^{-\frac52}\right)}^{\text{äußere Abl.}}\cdot\overbrace{4x^3}^{\text{innere Abl.}}}_{=v'}$$Diesmal klammern wir \((5+x^4)^{-\frac52}\) aus:$$f''(x)=(5+x^4)^{-\frac52}\cdot\left(10\cdot(5+x^4)-10x\cdot\frac32\cdot4x^3\right)$$$$\phantom{f''(x)}=(5+x^4)^{-\frac52}\cdot\left(50+10x^4-60x^4\right)$$$$\phantom{f''(x)}=\frac{50-50x^4}{(5+x^4)^\frac52}=-\frac{50(x^4-1)}{(5+x^4)^\frac52}$$

Answer 2

\( f(x)=\frac{x^{2}}{\sqrt{5+x^{2}}} \)
\( \frac{d f(x)}{d x}=\frac{2 x \cdot \sqrt{5+x^{2}}-\frac{x^{2} \cdot 2 x}{2 \cdot \sqrt{5+x^{2}}}}{5+x^{2}}=\frac{2 x \cdot \sqrt{5+x^{2}}-\frac{x^{3}}{\sqrt{5+x^{2}}}}{5+x^{2}}= \)
\( =\frac{2 x \cdot \sqrt{5+x^{2}} \cdot \sqrt{5+x^{2}}-x^{3}}{\left(5+x^{2}\right) \cdot \sqrt{5+x^{2}}}= \)
\( =\frac{\left(2 x \cdot\left(5+x^{2}\right)-x^{3}\right)}{\left(5+x^{2}\right) \cdot \sqrt{5+x^{2}}}= \)
\( =\frac{10 x+2 x^{3}-x^{3}}{\left(5+x^{2}\right) \cdot \sqrt{5+x^{2}}}=\frac{10 x+x^{3}}{\left(5+x^{2}\right) \cdot \sqrt{5+x^{2}}} \)

Comments

Du hast aus Versehen den Nenner falsch übernommen.

In der Aufgabe steht dort ein \(x^4\), kein \(x^2\)...

---

Danke für den Hinweis!

Answer 3

Du kannst 2x*(5+x^4)^(-1/2) ausklammern.

Comments

Ich komme leider so immer noch nicht weiter :(

---

Klammere das Genannte aus und kürze damit!

a^(-1/2)/a = 1/a^(3/2)

Answer 4

Verwende https://www.ableitungsrechner.net/ zur Hilfe und Selbstkontrolle