Aufgabe:
Die Ölfirma Schnell fördert Öl mittels 20 identischer Plattformen. Die Ölfirma produziert unter der Kostenfunktion
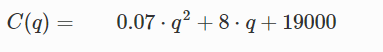
Text erkannt:
\( C(q)=0.07 \cdot q^{2}+8 \cdot q+19000 \)
wobei q die Gesamtmenge der geförderten Megabarrel (Mbbl) Öl bezeichnet.
Bei einem Preis von 24 GE beträgt die nachgefragte Menge 2999.4 und bei einem Preis von 34 GE beträgt die nachgefragte Menge 2905.4.
Stellen Sie die lineare Nachfragefunktion als Funktion des Preises sowie die inverse Nachfragefunktion als Funktion der Menge auf und führen Sie eine Gewinnoptimierung durch. Ermitteln Sie dann folgende Größen:
a. Steigung der Nachfragefunktion:
-9.4
b. Preis, bei dem die Nachfrage verschwindet:
343.09
c. Nachfrage pro Plattform im Gewinnoptimum:
47.49
d. Preis im Gewinnoptimum:
242.03
e. Maximal erzielbarer Gewinn:
140145.22
f. Gesamtkosten im Gewinnoptimum:
89757.99
Problem/Ansatz:
Ich konnte alle Lösen jedoch komme ich bei der d nicht auf 242,03 kann mir jemand eventuell bitte helfen?