Mit TdV nicht möglich, oder?
Und mega Danke, nur kommt da nicht:
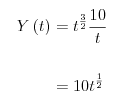 raus?
raus?

Text erkannt:
Einsetzung in die allgemeine Formel zur Lösung einer inhomogen linearen Differentialgleichung:
\( Y(t)=e^{-\left(-\frac{3}{2} \ln |t|\right)}\left(c+\int e^{-\frac{3}{2} \ln (t)} \cdot\left(-\frac{10}{\sqrt{t}}\right) d t\right) \)
Berechnung des Integrals:
\( \begin{aligned} \int e^{-\frac{3}{2} \ln (t)} \cdot\left(-\frac{10}{\sqrt{t}}\right) d t &=\int-10 \cdot t^{-\frac{3}{2}} t^{-\frac{1}{2}} d t \\ &=\int-10 t^{-2} d t \\ &=\frac{10}{t} \end{aligned} \)
Fortführung der Berechnung der Differentialgleichung:
\( \begin{aligned} Y(t) &=e^{-\left(-\frac{3}{2} \ln |t|\right)}\left(c+\frac{10}{t}\right) \\ &=t^{\frac{3}{2}}\left(c+\frac{10}{t}\right) \end{aligned} \)
Bestimmung der speziellen Lösung mit der Anfangsbedingung \( Y(1)=10 \) :
\( \begin{aligned} y(1) &=10 \\ \Leftrightarrow 1^{\frac{3}{2}}\left(c+\frac{10}{1}\right) &=10 \\ \Leftrightarrow c &=0 \end{aligned} \)
\( \begin{aligned} Y(t) &=t^{\frac{3}{2}} \frac{10}{t} \\ &=10 t^{\frac{1}{2}} \end{aligned} \)