Hallo,
hier findest du einen "Übersetzer" für Steckbriefaufgaben. Es gibt sicherlich auch noch andere Seiten, die evtl. mehr Erläuterungen liefern.
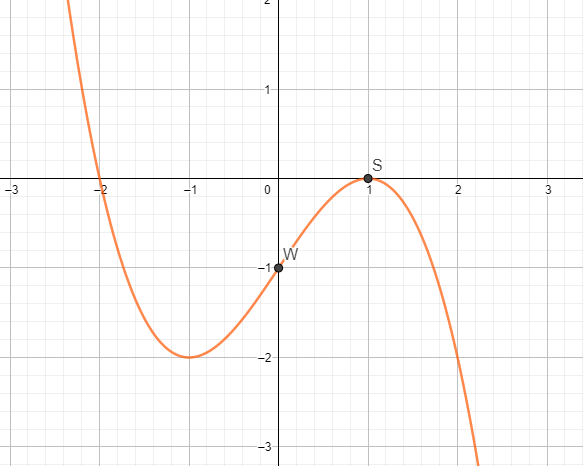
Bestimme die Gleichung einer ganzrationalen Funktion 3. Grades, deren Graph in S(1/0) die x- Achse berührt und in W(0/-1) einen Wendepunkt hat.
Eine Funktion 3. Grades und die ersten beiden Ableitungen kannst du so schreiben:
\(f(x)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+2bx+c\\ f''(x)=6ax +2b\)
Du brauchst 4 Gleichungen, um a, b, c und d zu bestimmen.
Aus der Information "deren Graph in S(1/0) die x- Achse berührt" folgt
\(f(1)=0\Rightarrow a+b+c+d=0\\ f'(x)=0\Rightarrow 3a+2b+c=0\)
"W(0/-1) einen Wendepunkt hat." liefert
\(f(0)=-1\Rightarrow d=-1\\ f''(0)=0\Rightarrow b=0\)
Damit weißt du \(f(x)=ax^3+cx-1\)
Und die ersten beiden Gleichungen sind nun
\(a+c-1=0\\ 3a+c=0\)
Die Lösung dieses Gleichungsstems ist a = -0,5 und c = 1,5
\(f(x)=-0,5x^3+1,5x-1\)
Melde dich, falls du dazu noch Fragen hast.
Gruß, Silvia