Binomischer Lehrsatz - Beispiel

Question

Aufgabe:

Problem/Ansatz:

Man soll folgenden Ausdruck bestimmen:

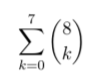
Text erkannt:

\( \sum \limits_{k=0}^{7}\left(\begin{array}{l}8 \\ k\end{array}\right) \)

Meine Überlegung:

wegen n!/(n-k)k! soll der Ausdruck gleich 8!/(8-k)k! - das hätte ich dann berechnet.

Normalerweise dürfen wir aber keine Taschenrechner benüzten und händisch wäre die Berechnung etwas lang.

Lässt sich diese Aufgabe anderst überlegen?

Danke für alle Tipps!

Answer 1

Nach besagtem Satz ist$$(1+1)^n=\sum_{k=0}^n\binom nk\cdot1^{n-k}\cdot1^k=\sum_{k=0}^n\binom nk.$$Mit \(n=8\) folgt daraus$$\sum_{k=0}^7\binom8k=\sum_{k=0}^8\binom8k-\binom88=(1+1)^8-1=2^8-1=255.$$

Answer 2

1+ 8+28+ 56+70+ 56+28+ 8=255

Answer 3

Du kannst ja auf ( 1+1)⁸ den binomischen Satz anwenden, dann gibt das

\(  2^8 =  \begin{pmatrix} 8\\0 \end{pmatrix}  +  \begin{pmatrix} 8\\1 \end{pmatrix} +...+  \begin{pmatrix} 8\\8 \end{pmatrix} \)

und der letzte Summand ist 1, also gibt die Summe bis k=7 nur 255.