Wie komme ich von dieser Geraden zu einer Ebene?

Question

Aufgabe:

Geben Sie die Gleichung einer Ebene an, die senkrecht auf E: 2x + 2y + 3z =6 steht und den Punkt (1/1/1) enthält.

Problem/Ansatz:

Hallo!

Zuerst hatte ich die Aufgabe falsch gelesen und eine Gerade senkrecht zu E durch den Punkt berechnet:

g:x = \( \begin{pmatrix} 1\\1\\1 \end{pmatrix} \)+r × \( \begin{pmatrix} 2\\2\\3 \end{pmatrix} \)

Wie komme ich von dieser Geraden zu einer Ebene?

LG Emi

Answer 1

Jede Ebene, die den Normalenvektor deiner gegebenen Ebene als einien ihrer beiden Spannvektoren besitzt, ist senkrecht zu deiner gegebenen Ebene.

Comments

Heißt das, ich kann mir einen weiteren Spannvektoren einfach ausdenken?

---

Ja, genau das bedeutet es.

---

Heißt das, ich kann mir einen weiteren Spannvektoren einfach ausdenken?

wie abakus schon schrieb: Ja

ich habe das noch mal in den Geoknecht3D gegossen:

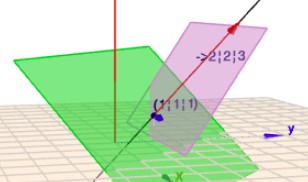
Die schwarze Gerade ist die Gerade \(g\), deren Richtungsvektor ich rot markiert habe. Jede Ebene, die \(g\) enthält, steht zwangsläufig senkrecht auf der Ebene \(E\) (grün) aus der Aufgabe.

Ich habe hier als zweiten Spanvektor \((1|\,0|\,0)\) gewählt (blau), was dann zu der lila Ebene führt. Denke Dir die Gerade \(g\) als eine Drehachse. Die lila Ebene kann um \(g\) gedreht werden, sie steht immer senkrecht auf \(E\).

(klick auf das Bild, dann siehst Du es besser)

---

Vielen Dank für die graphische Antwort!

Answer 2

Da nehmen wir einen Vektor der senkrecht zu (2,2,3), z.B. (1,-1,0) und bringen den mit P zusammen

(1,-1,0)^T ((x,y,z)^T-(1,1,1)^T)=0

fertisch

Comments

Wofür steht das hoch T?

---

Das steht für Transponieren, schreibe Zeilen-Punkte als Spalten-Vektoren

---

Das steht für Transponieren, ...

dann sollte man den ersten Vektor aber ohne hoch-T schreiben, denn der ist ein Zeilenvektor. Sonst wird da kein Skalarprodukt draus:

(1,-1,0) ((x,y,z)^T-(1,1,1)^T)=0   heißt$$\begin{pmatrix}1& -1& 0\end{pmatrix}\left(\begin{pmatrix}x\\ y\\ z\end{pmatrix} - \begin{pmatrix}1\\ 1\\ 1\end{pmatrix}\right)=0$$