welche Werte soll ich für die pq Formel nun verwenden?

Question

Hallo,

ich muss diese Funktion:

f(x) = 0,1x³ + 0,3x² - 0,9x + 0,5

auf ihre Symmetrie, Nullstellen, Extrempunkte und Wendepunkte untersuchen.

1. Erkenntnis: Keine Symmetrie!

2. Nullstellen berechnen: Wenn ich die Funktion =0 setze und dann sozusagen ausklammere steht dort :

x( 0,1x² + 0,3x -0,9 + 0,5)

welche Werte soll ich für die pq Formel nun verwenden? Die letzten beiden Werte oder wie entscheidet man das?

Vielen Dank im Voraus!

Answer 1

Nullstellen

f(x) = 0.1·x^3 + 0.3·x^2 - 0.9·x + 0.5 = 0.1·(x^3 + 3·x^2 - 9·x + 5) = 0

Eine Nullstelle bei 1 weil de Summe der Koeffizienten 0 ist. Dann Polynomdivision bzw. Horner Schema

(x^3 + 3·x^2 - 9·x + 5)/(x - 1) = x^2 + 4·x - 5 = (x - 1)·(x + 5) = 0

x = 1 x = -5

Also sind die Nullstellen x = -5 (einfach) ∨ x = 1 (zweifach)

Answer 2

Du kannst x so nicht ausklammern. 0,5 hat keinen Faktor x bei sich.

Multipliziere die Gleichung mit 10:

x^3+3x^2-9x+5 = 0

Polynomdivision, Nullstelle raten

x= 1 ist Nullstelle.

(x^3+3x^2-9x+5) : (x-1) = ...

Answer 3

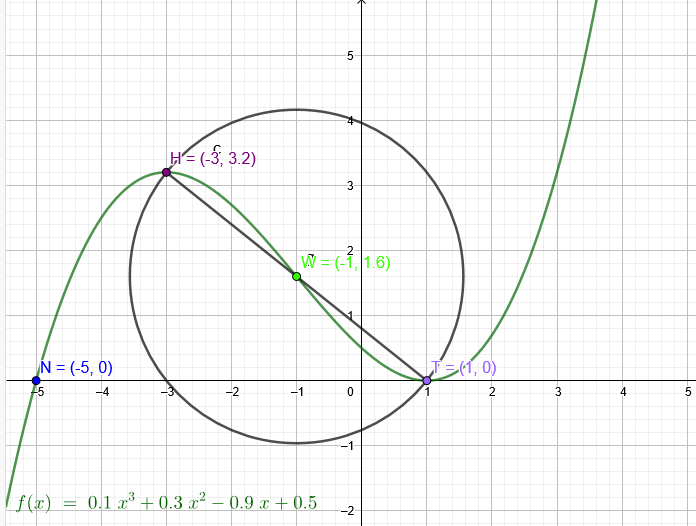
f(x) = 0,1x³ + 0,3x² - 0,9x + 0,5

f´(x)=0,3x^2+0,6x-0,9

0,3x^2+0,6x-0,9=0  |:0,3

x^2+2x-3=0

x^2+2x=3

(x+1)^2=3+1=4 \( \sqrt{} \) |

1.)x+1=2

x₁=1    f(1) = 0,1 + 0,3 - 0,9 + 0,5=0  Somit auch Nullstelle.

2.)x+1=-2

x₂=-3    f(-3) = 0,1*(-3)³ + 0,3*(-3)² - 0,9(-3) + 0,5=3,2

f´´(x)=0,6x+0,6

Art der Extrema:

f´´(1)=0,6+0,6=1,2>0 Minimum

f´´(-3)=0,6*(-3)+0,6=-1,2<0Maximum

Wendepunkt:

0,6x+0,6=0

x=-1    f(-1) =1,6

Der Wendepunkt liegt "in der Mitte" zwischen Maximum und Minimum.