
Bitte hilft ihr mir bei der Umwandlung der Gerade in den Normalvektorform.
Bei mir kommt alles so vor :
Zuerst Parameterdarstellung
X= A +t*(AP)
AP= (2,1)-(-2,-1)=(4,2)
X=(-2,-1)+t*(4,2)
Geogebra zeigt mir folgendes :
Jetzt wollen wir die Parameterdarstellung der Gerade in Normalform umwandeln:
nX=nA
n=gekippte AP=(4,-2)
(4,-2)*(x,y)=(4,-2)(-2,-1)
4x-2y=-8+2
4x-2y=-6
2x-y=-3
y=2x+3
und jetzt das Interessanteste: wenn ich solche Parametern in Geogebra eintippe, zeigt dieser höllische Rechner folgende Abbildung:
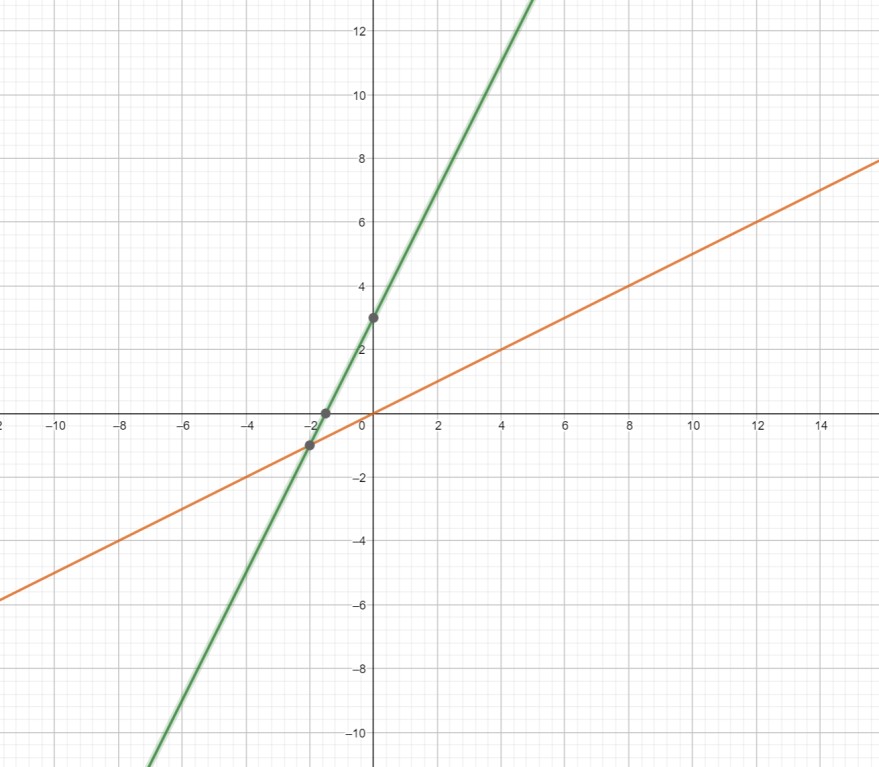
HHier stellt sich die Frage heraus: wo habe ich mich vertan? Danke für irgendeine Hilfe im Voraus!