Aufgabe:
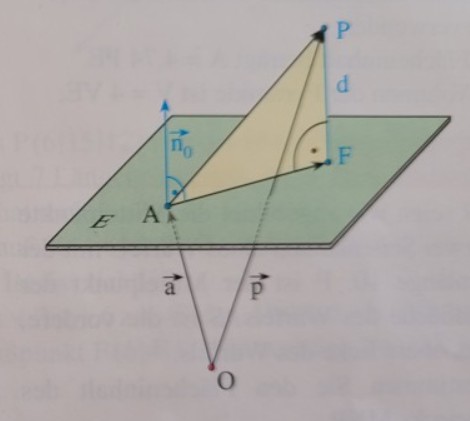
Begründung der Abstandsformel:
P sei ein Punkt, der auf derjenigen Seite der Ebene \( \mathrm{E} \) liegt, nach der \( \overrightarrow{\mathrm{n}}_{0} \) zeigt. Dann gilt folgende Rechnung:
\( \begin{array}{l} (\overrightarrow{\mathrm{p}}-\overrightarrow{\mathrm{a}}) \cdot \overrightarrow{\mathrm{n}}_{0}=\overrightarrow{\mathrm{AP}} \cdot \overrightarrow{\mathrm{n}}_{0}=(\overrightarrow{\mathrm{AF}}+\overrightarrow{\mathrm{FP}}) \cdot \overrightarrow{\mathrm{n}}_{0} \\ =\overrightarrow{\mathrm{AF}} \cdot \overrightarrow{\mathrm{n}}_{0}+\overrightarrow{\mathrm{FP}} \cdot \overrightarrow{\mathrm{n}}_{0} \\ =|\overrightarrow{\mathrm{AF}}| \cdot\left|\overrightarrow{\mathrm{n}}_{0}\right| \cdot \cos 90^{\circ}+|\overrightarrow{\mathrm{FP}}| \cdot\left|\overrightarrow{\mathrm{n}}_{0}\right| \cdot \cos 0^{\circ} \\ =|\overrightarrow{\mathrm{FP}}|=d \end{array} \)
\( (\overrightarrow{\mathrm{p}}-\overrightarrow{\mathrm{a}}) \cdot \overrightarrow{\mathrm{n}}_{0}=\overrightarrow{\mathrm{AP}} \cdot \overrightarrow{\mathrm{n}}_{0}=(\overrightarrow{\mathrm{AF}}+\overrightarrow{\mathrm{FP}}) \cdot \overrightarrow{\mathrm{n}}_{0} \) \( =\overrightarrow{\mathrm{AF}} \cdot \overrightarrow{\mathrm{n}}_{0}+\overrightarrow{\mathrm{FP}} \cdot \overrightarrow{\mathrm{n}}_{0} \) \( =|\overrightarrow{\mathrm{AF}}| \cdot\left|\overrightarrow{\mathrm{n}}_{0}\right| \cdot \cos 90^{\circ}+|\overrightarrow{\mathrm{FP}}| \cdot\left|\overrightarrow{\mathrm{n}}_{0}\right| \cdot \cos 0^{\circ} \) \( =|\overrightarrow{\mathrm{FP}}|=\mathrm{d} \)
Liegt \( \mathrm{P} \) auf der anderen Seite von E, so ergibt \( \operatorname{sich}(\overrightarrow{\mathrm{p}}-\overrightarrow{\mathrm{a}}) \cdot \overrightarrow{\mathrm{n}}_{0}=-d \).
Insgesamt: \( d=\left|(\vec{p}-\vec{a}) \cdot \vec{n}_{0}\right| \).
Problem/Ansatz:
Hallo Freunde,
Ich habe von meinem Mathelehrer die Aufgabe bekommen, die Begründung der Hesseschen Abstandsformel nur Mithilfe der Abbildung zu erklären. Einiges ist mir klar, jedoch würde ich freuen, wenn ihr mir das komplett erklären könntet, damit ich es präsentieren kann. Die Erklärung und Abbildung findet ihr im Bild.
Vielen Dank schonmal