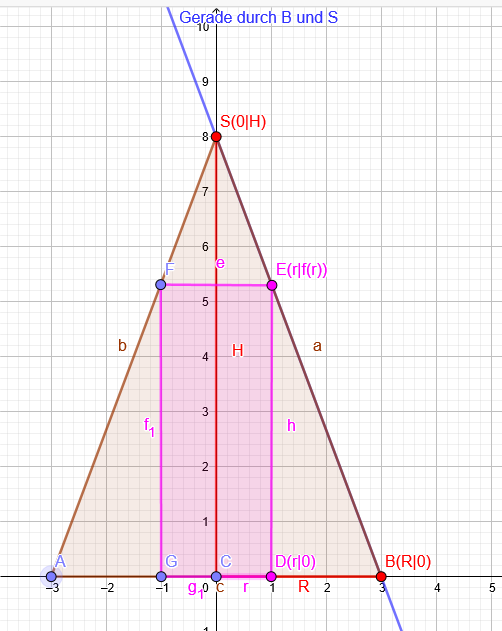
"Aufgabe: Einem geraden Kreiskegel mit dem Radius R und der Höhe H soll ein Kreiszylinder mit möglichst großem Volumen einbeschrieben werden."
\(V= r^{2}*π*h\) soll maximal werden.
Benennungen kannst du der Zeichnung entnehmen:
Gerade durch B(R|0) und S(0|H):
Bestimmung der Gleichung über die Achsenabschnittsform der Geraden:
Allgemein: \(\frac{x}{a}+\frac{y}{b}=1\)
Hier ist \(a=R\) und \(b=H\)
\(\frac{x}{R}+\frac{y}{H}=1\)
\(y=-\frac{H}{R}*x+H\)
\(y(r)=-\frac{H}{R}*r+H\)
Nun ist \(y(r)=h\)
\(V= r^{2}*π*y(r)\)
\(V= r^{2}*π*(-\frac{H}{R}*r+H)\)
\(V=- r^{3}*π*\frac{H}{R}+ r^{2}*π*H\)
\(V´=-3 r^{2}*π*\frac{H}{R}+ 2r*π*H\)
\(-3 r^{2}*π*\frac{H}{R}+ 2r*π*H=0\)
\(r₁=0\)
\(r₂=\frac{2}{3}*R\)
\(h=\frac{1}{3}*H\)
\(V= \frac{4}{9}*R^{2}*π*\frac{1}{3}*H\)
\(V= \frac{4}{27}*R^{2}*π*H\)