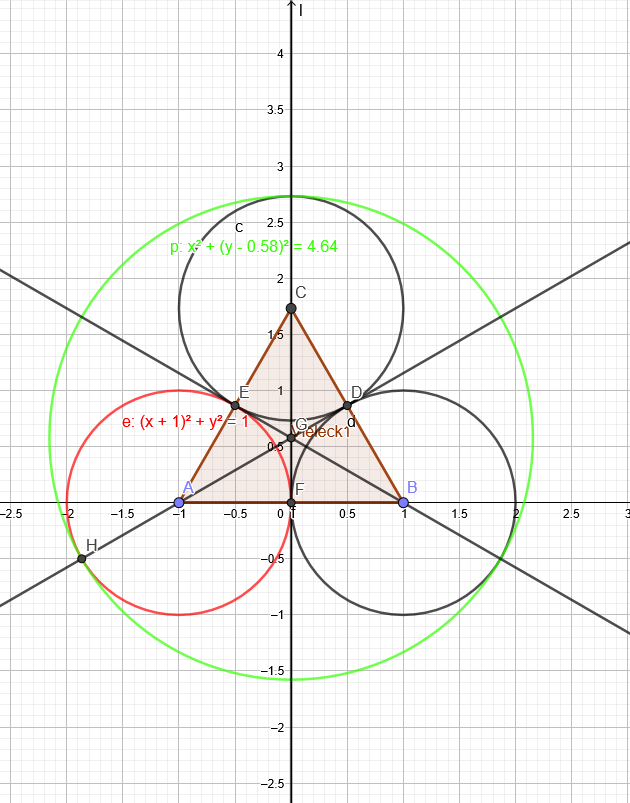
Ich gehe mal den umgekehrten Weg: von den 3 Kleinkreisen zum Großkreis:
Bei einem Großkreisradius von \(R= \sqrt{4,64}≈2,15407\) hat ein innerer Kleinkreis einen Radius von \(r=1\)
\(A=R^{2}*π\)
\(A=4,64*π\)
Ein Kleinkreis hat eine Fläche von \(A=π\)
3 Kleinkreise somit \(A=3*π\)
Inhalt der gesuchten Fläche \(A=4,64*π-3*π=1,64*π\)