Der Abstand zum Quadrat von (0 | 7) zum Punkt (x | x^2) beträgt laut Pythagoras
d^2 = (x^2 - 7)^2 + (x - 0)^2 = x^4 - 14x^2 + 49 + x^2 = x^4 - 13x^2 + 49
Wenn der Abstand minimal ist ist auch das Quadrat minimal und damit muss die Ableitung von d^2 = 0 sein.
d^2' = 4x^3 - 26x = 0
x(4x^2 - 26) = 0
x = 0
4x^2 - 26 = 0
x = √26/2
Aus Symmetriegründen brauch ich nur den positiven Wert betrachten.
Bei x = 0 wäre d^2 = 49
Bei x = √26/2 wäre d^2 = 6,75
Bei x = √26/2 ist der Abstand minimal.
Der Abstand beträgt dann:
d^2 = 6,75
d = √6,75 = 3/2·√3 = 2,598
P(√26/2 | 6,5) ~~ P(2,550 | 6,5)
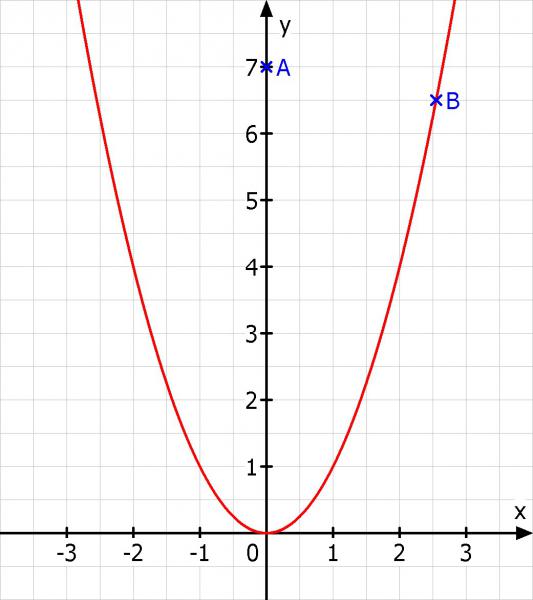
Hier noch eine Skizze.