Anteil der gefärbten Fläche bestimmen

Question

Liebe Forum-Mitglieder,

Aufgabe:

In der Figur ist M die Mitte der Rechtecksseite. Bestimme den Anteil der gefärbten Fläche an der Rechtecksfläche.

Problem/Ansatz:

Diese Aufgabe wurde unter dem Thema "Eigenschaften ähnlicher Figuren" gestellt. Ich verstehe aber nicht, wie ich mit dem Beweis einer Ahnlichkeit der Dreiecke den Flächeninhalt herausfinden soll. Wie soll ich eine Fläche ohne jegliche Angaben berechnen?

LG                                                                                                                                                                                             Orbi

Answer 1

Hallo,

Wie soll ich eine Fläche ohne jegliche Angaben berechnen?

Die Angaben sind vollständig vorhanden. Es ist ja 'nur' nach dem Anteil der Fläche des gelben Dreiecks an der Fläche des Rechtecks gefragt.

Diese Aufgabe wurde unter dem Thema "Eigenschaften ähnlicher Figuren" gestellt.

Die drei Strecken im Rechteck teilen die Fläche in insgesamt fünf Dreiecke. Von diesen fünf Dreiecken sind genau zwei ähnlich.

Nämlich \(\triangle AME\) und \(\triangle CDE\). Und da \(|AM| = \frac12 |CD|\) muss auch \(|ME|=\frac12|ED|\) sein. Bzw.$$|ME| = \frac13|MD|$$Das bedeutet für die Flächen$$F_{\triangle EMC} = \frac13 F_{\triangle DMC} = \frac13 \cdot \frac 12 F_R = \frac 16F_R$$wenn \(F_R\) die Fläche des Rechtecks ist.

Gruß Werner

Answer 2

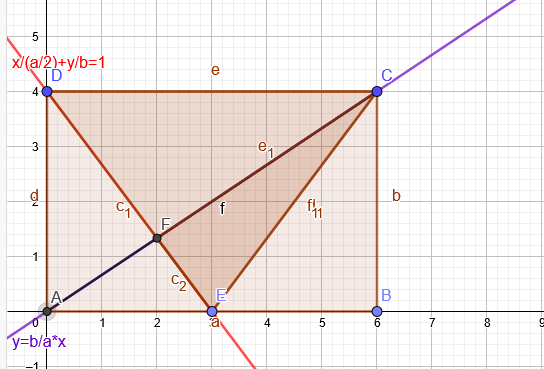
Berechnungsweg ohne "Eigenschaften ähnlicher Figuren" :

Benennungen sind in der Zeichnung ersichtlich

\(Fläche Dreieck ABC= \frac{1}{2}*a*b \)

\(Gerade durch AC: y= \frac{b}{a}*x\)

\(Gerade durch ED: \frac{2x}{a}+\frac{y}{b}=1\)

\(Gerade durch ED: y=b-\frac{2bx}{a}\)

\(Schnitt   beider   Geraden: \frac{b}{a}*x = b-\frac{2bx}{a}\)

\(Schnitt   beider   Geraden: x = \frac{a}{3}\)

\(Schnitt beider Geraden: y = \frac{b}{3}\)

\(Fläche Dreieck AEF= \frac{1}{12}*a*b \)

\(Fläche Dreieck EBD= \frac{1}{4}*a*b \)

\(gesuchte  Fläche  CEF \):

\(\frac{1}{2}*a*b-\frac{1}{4}*a*b-\frac{1}{12}*a*b=\frac{1}{6}*a*b\)

Comments

Gute Idee, kann man so machen.

Pluspunkt!

Nur interessehalber: Gerade AC wurde gleich in Normalform angegeben.

Die Gerade ED wurde erst in Achsenabschnittsform angegeben, danach erst in Normalform umgewandelt. Steckt eine spezielle Intention in diesem unterschiedlichen Vorgehen?

---

"Die Gerade ED wurde erst in Achsenabschnittsform angegeben, danach erst in Normalform umgewandelt. Steckt eine spezielle Intention in diesem unterschiedlichen Vorgehen?"

Danke dir für den Pluspunkt!

Ich habe die Achsenabschnittsform gewählt, da die Abschnitte gleich ersichtlich sind.

Answer 3

Ähnlich sind die Dreiecke AMB und BCD. h=a/3 (mit Strahlensatz). Das Flächenverhältnis von AMB und BCD 1:4.

Jetzt kannst du alle Flächen in Abhängigkeit von a und b=|DC| bestimmen.

Answer 4

Kannst auch das ganze Rechteck (Breite b , Höhe a) durch

eine Symmetrieachse durch M halbieren.

Dann wird die gefärbte Fläche in zwei Teile geteilt.

Der links Teil ist ein Dreieck mit Grundseite a/2 und

Höhe b/6 , also A = ab/24.

Und der rechte Teil ist die Differenz der halben Rechteckshälfte und

des darüber liegenden Dreiecks

A = ab/4 - ab/8 = ab/8

gefärbte Fläche insgesamt also ab/24 + ab/8 = ab/6 ,

also 1/6 der Rechtecksfläche.