Hallo,
Willkommen in der Mathelounge!
mache Dir solche Aufgaben immer am Einheitskreis klar.
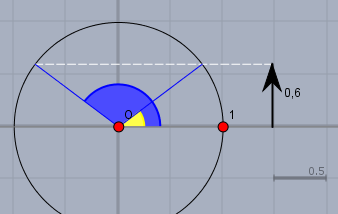
Die Parallele zur Horizontalen im Abstand 0,6 schneidet den Kreis 2-mal. Es gibt also zwei Winkel \(x_1\) und \(x_2\) für die gilt$$\sin(x_{1,2}) = 0,6$$ Berechne zunächst den gelben Winkel, den spuckt Dein Taschenrechner aus, wenn Du die Umkehrfunktion des Sinus \(\sin^{-1}\) bzw. \(\arcsin\) nutzt. Das ist ungefähr$$\sin(x_1) = 0,6 \implies x_1 \approx 36,9°$$und den zweiten (blauen) Winkel erhältst Du, indem Du von 180° den ersten abziehst:$$x_2 = 180° - x_1$$Beide Winkel liegen im geforderten Intervall von \([0;\,2\pi)\) bzw. \([0°;\, 360°)\).
Gruß Werner