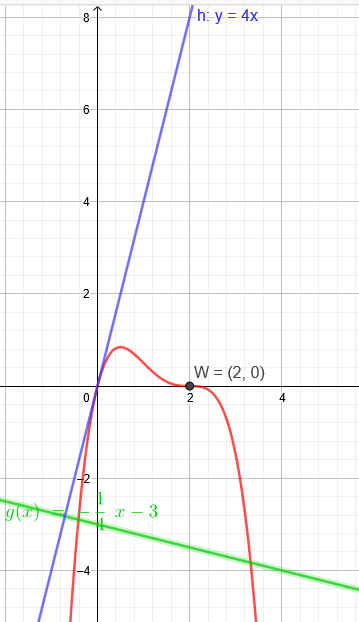
Eine ganzrationale Funktion 4. Grades hat im Wendepunkt W (2| 0) eine
horizontale Tangente. Sie verläuft durch den Ursprung.
Die Tangente im Ursprung ist senkrecht zur Geraden \(y = - \frac{1}{4} x - 3\) Normale durch den Ursprung: \(y = 4x \)
\(f(x)=a*[x*(x-2)^3]\)
\(f´(x)=a*[(x-2)^3+x*3*(x-2)^2*1]\)
\(f´(0)=a*(0-2)^3=-8a→-8a=4→a=-\frac{1}{2}\)
\(f(x)=-\frac{1}{2}*x*(x-2)^3\)