Differentialrechnung Körper

Question

Aufgabe: Zum Schutz gegen mechanische Beschädigungen werden unterirdisch verlegte Kabel
mit Formstücken aus Beton so abgeschirmt, daß die Kabel in einem Hohlraum liegen
(7 Bild C69). Der Hohlraum soll eine rechteckige Querschnittsfläche von 18 dm?
Inhalt haben. Wand- und Deckenstärke betragen jeweils 1 dm. Für die Herstellung der
Formstücke soll möglichst wenig Beton verbraucht werden, das heißt, der Inhalt der in
der Skizze dunkelblau gefärbten Fläche soll minimal werden. Berechnen Sie für diesen
Fall die Abmessungen a und h der Querschnittsfläche des Hohlraumes.

Text erkannt:

7

Problem/Ansatz: Ich habe Probleme mit dem Ansatz sowie dem Verständnis. Hat jemand einen kompletten nachvollziehbaren Lösungsweg für mich?

Comments

Differentialrechnung Körper

Es geht nicht um einen Körper sondern um eine Fläche, nämlich den Querschnitt des Körpers.

Answer 1

Die Fläche berechnet sich zu $$ (1) \quad A = a h = 18  $$ und der Materialverbrauch zu $$ (2) \quad M = (2h + 2 + a) L $$ wobei \( L \) die Tiefe des Betonstück ist.

Es soll so wenig wie möglich Material verbraucht werden, durch einsetzten von (1) in (2) folgt

$$ M(a) = \left( \frac{36}{a} + 2 +a \right) L $$

Also muss gelten $$ \frac{d M}{da} = 0 $$ gelten und daraus folgt \( a = 6 \)

Comments

Ich weiß, die Frage ist ein bisschen spät, wohin verschwindet denn das angegebene L?

---

Hatte das \( L \) vergessen. Ändert aber nichts am Rechenweg, da \( L \) als Konstante dann bei der Divison wegfällt. Hab das oben ergänzt.

Answer 2

alle nachfolgenden Zahlen in dm bzw. dm²

Die Querschnittsfläche beträgt a+2 (im Bild rot) + 2b (im Bild dunkelblau):

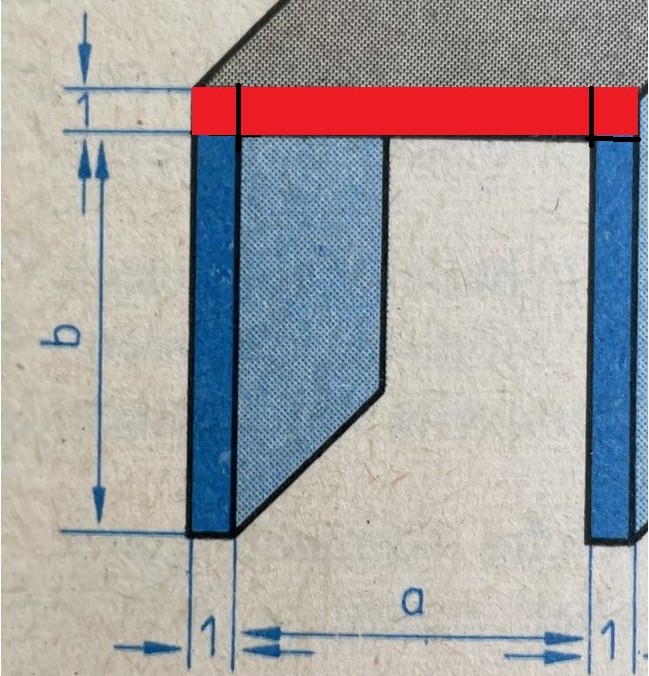
Weil a*b = 18 gilt b = 18/a und es kann der Flächeninhalt F mit einer Variablen geschrieben werden als F(a) = a+2 + 2*18/a

Da Du davon das Minimum suchst, muss die erste Ableitung gleich null gesetzt werden:

1 - 36/a² = 0

Daraus folgt a = 6 und es gilt b = 18/a