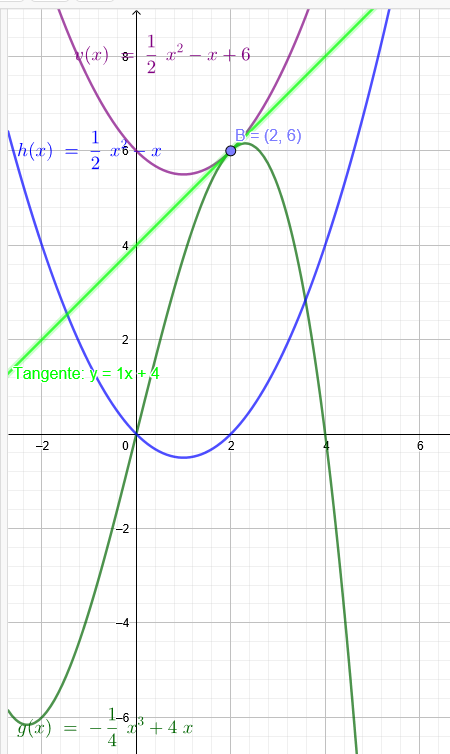
Gegeben: \(g(x)= -\frac{1}{4}*x^{3} +4x\)
\(h(x)= \frac{1}{2}*x^{2} - x\)
Der Graph von h kann so nach oben verschoben werden dass er den Graphen von g an der Stelle x=2 berührt. Der verschobene Graph sei v
\(g(2)= -\frac{1}{4}*2^{3} +4*2=6\)
\(v(x)= \frac{1}{2}*x^{2} - x+6\)
Nachweis Berührpunkt:
\(g(2)=v(2) \)
\(g´(2)=v´(2) \)
\(g(2)= -\frac{1}{4}*2^{3} +4*2=6\)
\(v(2)= \frac{1}{2}*2^{2} - 2+6=6\)
\(g´(x)= -\frac{3}{4}*x^{2} +4\)
\(g´(2)= -\frac{3}{4}*2^{2} +4=1\)
\(v´(x)= x- 1\)
\(v´(2)= 2- 1=1\)