Text erkannt:
Prüfungsinhalt
Aufgabe B 1
Seit 2007 können Fußgänger aus der Altstadt den Stadthafen von Sassnitz uber den Gehweg einer zweiteiligen Bruckenkonstruktion erreichen
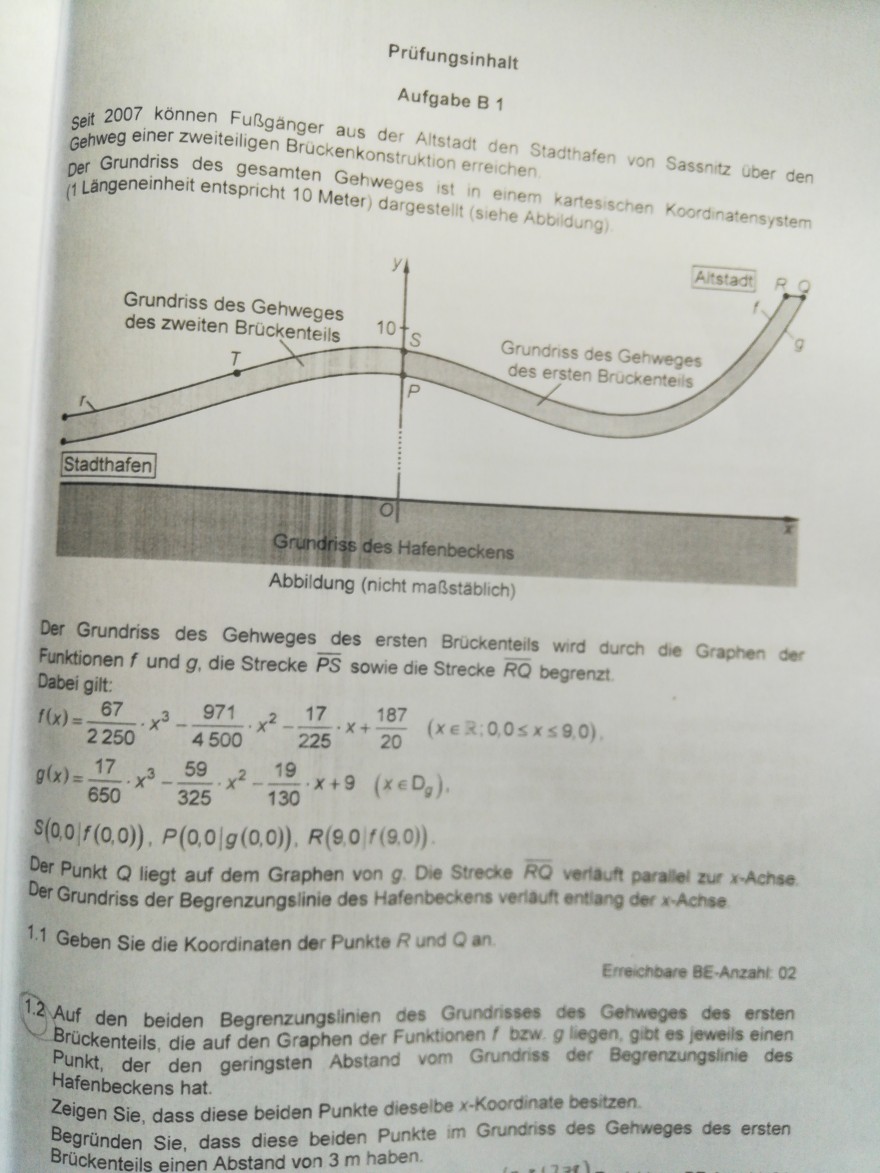
Der Grundriss des gesamten Gehweges ist in einem kartesischen Koordinatensystem (1 Längeneinheit entspricht 10 Meter) dargestellt (siehe Abbildung)
Der Grundriss des Gehweges des ersten Brückenteils wird durch die Graphen der Funktionen \( f \) und \( g \), die Strecke \( \overline{P S} \) sowie die Strecke \( \overline{R Q} \) begrenzt.
Dabei gilt:
\( \begin{array}{l} f(x)=\frac{67}{2250} \cdot x^{3}-\frac{971}{4500} \cdot x^{2}-\frac{17}{225} \cdot x+\frac{187}{20} \quad(x \in R ; 0,0 \leq x \leq 9,0) \\ g(x)=\frac{17}{650} \cdot x^{3}-\frac{59}{325} \cdot x^{2}-\frac{19}{130} \cdot x+9 \quad\left(x \in D_{g}\right) . \\ S(0,0 \mid f(0,0)), P(0,0 \mid g(0,0)), R(9,0 \mid f(9,0)) . \end{array} \)
Der Punkt \( Q \) liegt auf dem Graphen von \( g \). Die Strecke \( \overline{R Q} \) veriauft parallel zur \( x \)-Achse. Der Grundriss der Begrenzungslinie des Hafenbeckens veriauft entiang der \( x \)-Achse
1.1 Geben Sie die Koordinaten der Punkte \( R \) und \( Q \) an.
Erreichbare BE-Anzaht 02
1.2 Auf den beiden Begrenzungslinien des Grundrisses des Gehweges des ersten Brückenteils, die auf den Graphen der Funktionen \( f \) bzw. \( g \) liegen, gibt es jeweils einen Punkt, der den geringsten Abstand vom Grundriss der Begrenzungslinie des Hafenbeckens hat.
Zeigen Sie, dass diese beiden Punkte dieselbe \( x \)-Koordinate besitzen.
Begründen Sie, dass diese beiden Punkte im Grundriss des Gehweges des ersten Brückenteils einen Abstand von \( 3 \mathrm{~m} \) haben.
Text erkannt:
aus der Altstadt den Stadthafen von Sassnitz über den ckenkonstruktion erreichen.
רehweges ist in einem kartesischen Koordinatensystem Meter) dargestellt (siehe Abbildung).
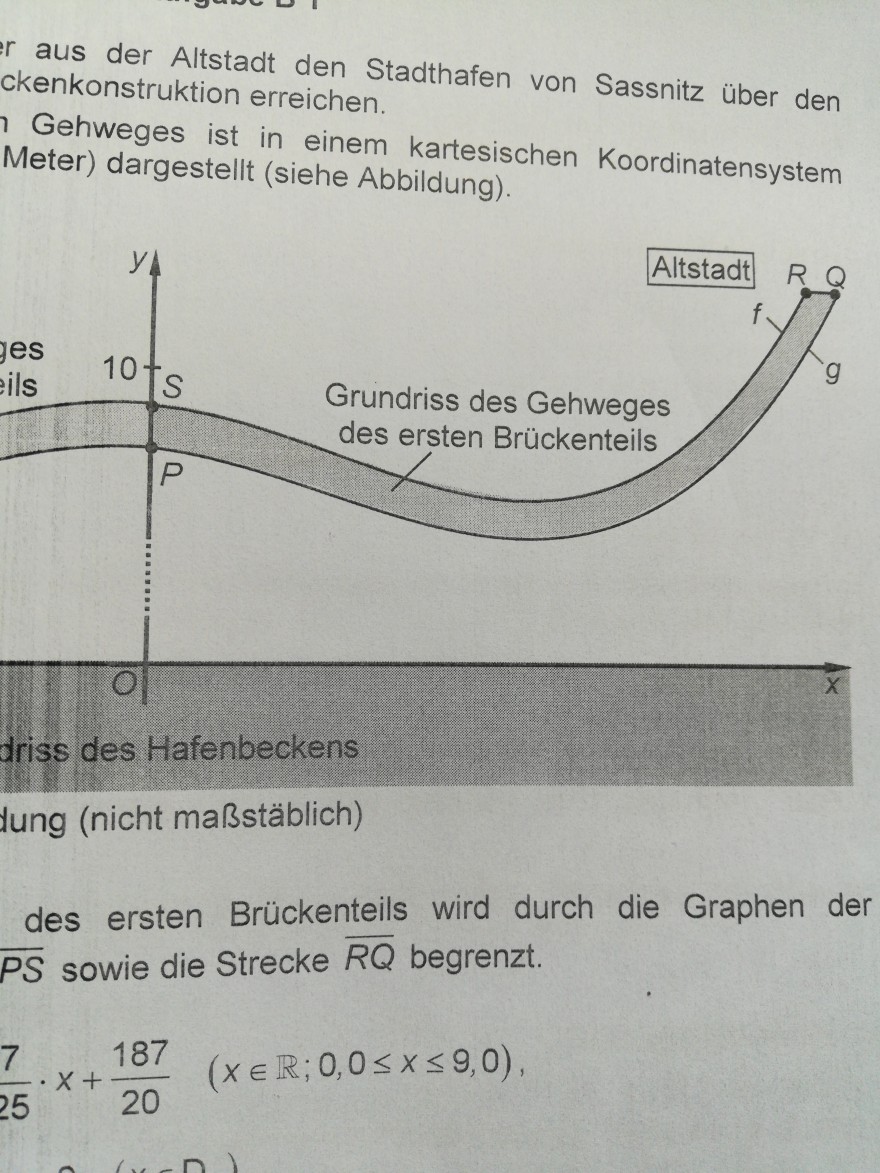
driss des Hafenbeckens
Hung (nicht maßstäblich)
des ersten Brückenteils wird durch die Graphen der \( \overline{P S} \) sowie die Strecke \( \overline{R Q} \) begrenzt.
\( \frac{7}{25} \cdot x+\frac{187}{20} \quad(x \in \mathbb{R} ; 0,0 \leq x \leq 9,0) \)
siehe skizze